· hashMap的数据结构

hashMap（散列表/哈希表）是一种提供键值映射关系数据结构，能做到高效查询key对应的value。它的底层结构是数组+链表，或者数组+树。

 

数组的每个元素都存储着一对或者多对key-value，key可以是字符串或者其他类型，数组的下标是整型，因此需要一个可以将key转为整型的hash函数，一般的思路是通过hash函数将一个key转为一个整型A后，再用整型A对数组的长度进行取模运算得到一个数组下标B。

 

当然，实际上很多高级语言或者应用都是用整型A与数组的长度掩码（即数组长度-1）进行&的位运算得到下标，因为对于计算机而言，位运算比取模要快得多。但是它们的实际效果是一样的，取模和&位运算都能得到相同的数组下标。当然了 A & (length - 1) 和 A mod length 等价的条件是 length必须是2的n次幂，而数组的长度一般都是2的n次幂。

 

hash函数应该满足2个要求：计算简单，极可能降低hash计算的复杂度；计算出来的hash值尽可能均匀分布。

 

·哈希表增删改查

 

查找

通过key寻找value的过程本质上是将key进行hash运算和位运算得到一个数组下标，根据数组下标、单个数组元素的大小和数组起始地址得到key所在下标的内存地址，并读取该内存地址的内容。

已知数组查找是随机访问，复杂度为O(1)，因此主要的复杂度来自哈希运算，现在计算机领域的哈希运算基本上都是O(1)的复杂度。因此综合起来，其查找复杂度可近似看做O(1)。

 

插入

以链表法构建的哈希表为例，插入操作也是需要先根据key找到数组对应的位置，对该数组位置下的链表链入新的value，其复杂度为O(1)。

 

删除

以链表法构建的哈希表为例，删除操作也是先查找到key对应的数组元素下的链表指针，从该链表中移除key节点。无需涉及到数组元素左移或右移，因此复杂度为O(1)。

 

修改

同查找，复杂度为O(1)。

 

· 解决冲突

插入时可能出现两个不同的key经过哈希运算和位运算之后得到一个相同的下标，此时发生冲突。

冲突则主流解决方法有 开放寻址法 和 链表法。

 

开放寻址法

（又称线性探测法）即如果新添加的某个key和之前的key发生冲突（计算出来的数组下标相同），就寻找下一个空的散列地址。直到散列表足够大，空的位置总能找到。

其公式如下：

某一个key的下标 = (该key哈希值 + 偏移量d) mod 数组长度

例如有一个集合{n1,..., n12}，集合中的元素计算出来的哈希值为{12,67,56,16,25,37,22,29,15,47,48,34}。现在他们要放入哈希表中，哈希表内数组长度为12。

.

当存储前5个数{12,67,56,16,25}时，都是没有冲突的散列地址:

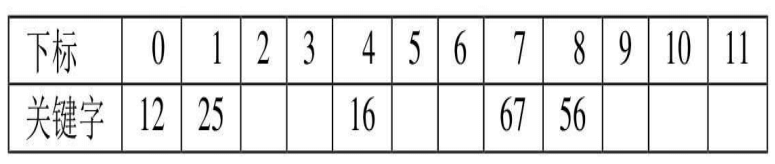
轮到37的时候，(37 + 0) mod 12 = 1，所以他应该放到arr[1]的位置，但是该位置已经被25占了。因此需要把偏移量+1并重新取模：(37+1) mod 12 = 2，arr[2]位置为空，因此37放到arr[2]中。如果偏移量自增后得到的下标仍被占用了，就再对偏移量自增，直到找到位置为空的下标。key和value的内容会被同时存到该下标中。

 

这种寻址法会随着数组中元素数量增大而效率降低，因为随着数组空闲位置数量的减少，一个key的插入可能会遇到多次冲突，寻址需要计算的次数会越来越多。

不仅是插入，连查询都要遵循上面的过程，如果偏移量d自增到数组长度的次数仍未查询到对应key，就说明这个key不存在于这个哈希表中。

因此，通过寻址法构建的哈希表查询不存在的key时，就会造成O(n)的复杂度。

 

而且在数组空闲位置数量越接近0时，插入和查找的复杂度也越接近O(n)。

为了避免这种情况，我们应该为数组初始化一个比较大的容量。

 

上面这种寻址方式是一次探测法。考虑一种情况，当数组如下图的时候：

如果某个key的hash为34，34 mod 12 = 10。找到arr[10]这个位置，但已经被占用。反而是他前一个位置arr[9]空闲, 那么就要需要再进行11次寻址计算才能找到arr[9]这个空闲位置：(34 + 11) mod 12 = 9，此时偏移量d需要自增到11才能找到正确的空闲位置。

 

优化方法是对偏移量考虑其相反数来计算，即偏移量d = 0, 1, -1, 2, -2...，这样偏移量改变到第2次是就能正确找到34的下标了。

我们称这种方法为二次探测法。

 

除此之外，我们可以通过生成不重复值的随机函数来获取一个随机偏移量，这种方式叫随机探测法。

上面这几种探测法都属于开放寻址法，只要数组有空闲位置就总能解决冲突。

 

 

链表法

 

链表法是让数组的每个元素存储一个单向链表（存链表的头指针），存储的key-value会作为一个节点对象存到数组元素中。如果某个key-value存入位置k发生冲突时，该key-value会作为尾部节点追加到arr[k]所存储的链表中（可能是追加到头部或尾部，追加到头部复杂度为O(1)，加到尾部复杂度为O(n)）。

 

链表法是目前最主流的解决哈希表冲突的方法，在不同的高级语言或应用中，数组元素保存的数据结构不同，有些使用单向链表，有些为了提高插入效率和查找效率使用红黑树，有些则使用双向链表。

 

 

再散列函数法

在插入和查找时使用多个散列函数而非一个散列函数。

插入时：使用第一个散列函数发生冲突则使用第二个散列函数，再冲突就用第三个散列函数，直到不冲突。但如果所有散列函数用完仍未找到空闲位置则冲突无法解决，因此需要结合其他解决冲突的方式一起使用。

 

查找时先使用第一个散列函数寻找key的下标，如果找到的key不是目标key则用第二散列函数寻找key的下标，直到找到的key与目标key匹配取出对应的value。如果执行完所有散列函数都没找到说明key不存在。

 

公共溢出区法

准备两个表：基本表和溢出表，基本表是一个hash表，溢出表则是一个普通的链表或者数组用来存储所有冲突的key。

插入时：通过计算hash值并取模找到数组下标，如果没冲突则key-value存入基本表的对应下标中。如果有冲突，则key-value存入溢出表中（存入溢出表的尾部）。

查找时：通过计算hash值并取模找到数组下标，在基本表的该下标找到key与目标key比对，如果两个key不符则再到溢出表找。此时需要遍历溢出表，用目标key与溢出表的key逐一比对直到找到一致的key。

 

在冲突很少的情况下，公共溢出表的查询性能也还是很高的。

 

 

·扩容

当哈希表的数组已经放满key-value之后，需要对哈希表进行扩容，否则哈希表插入和查询等操作效率会降低，并且无法解决冲突。

 

以Java中的哈希表为例，它的哈希表是以链表法构建的，决定一个哈希表是否扩容取决于HashMap的负载因子(用Lf表示，默认的Lf为0.75)。

 

负载因子 = HashMap中数组长度 / HashMap中链表节点数量

负载因子衡量的是每个数组下标平均存储k-v节点个数，也是每个数组下标的拥挤程度。如果有很多key因为解决冲突而放到同一数组下标的链表中，那么这个HashMap的负载因子就容易高。此时查询效率都会降低（因为链表的查询效率是O(n)），插入效率可能降低（要看插入到链表尾部还是头部）。

 

 

扩容的过程：

1. 底层会创建一个新的哈希表数组，该数组长度是原数组的2倍。
2. 对原有hashMap的所有节点rehash，即对所有key重新进行hash计算并放入到新数组的对应位置。数组长度变大后，求模得到每个key的数组下标会和之前不同。