连续分配的方式分配内存的最大缺点在于会产生很多内存碎片，内存利用率低（虽然可以通过紧凑技术解决，但是需要花费很多CPU时间），而产生很多内存碎片的根本原因在于必须为进程分配连续的内存空间（或者说进程会连续的存储在内存中）。

为什么连续存储会造成很多内存碎片？

因为对于较大的进程，系统要挑选大块的空闲空间给进程，很小块的空闲空间可能连较小的进程都无法容纳而永远无法被利用，就变成了内存碎片。

这样的事情多发生几次后就会产生很多碎片。

离散分配则允许为进程分配分散的内存块，即一个进程可以分布在不相邻的多个小分区中。

离散分配管理分为 分页存储、分段存储和段页式存储。

· 分页存储管理

分页存储是指 在物理上将内存空间分为多个大小相等的物理块，在逻辑上将进程的逻辑地址空间分为多个页面，每个页面和物理块一样大。OS分配和进程页面数量相同的物理块给进程，进程的页面可以离散的存放在内存的块中，与内存块一一对应，每个进程会维护一个逻辑页和物理块的页表表示几号页存在了几号块中。

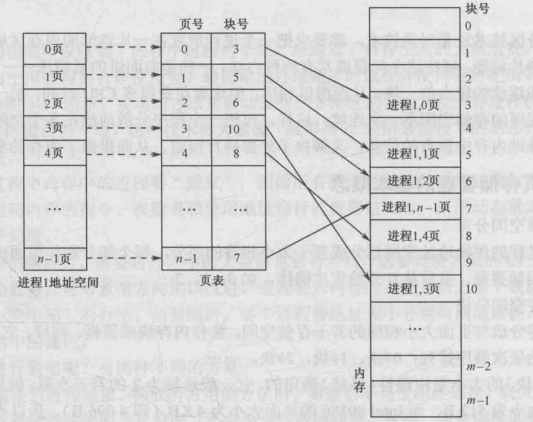
页面是逻辑空间单位，块是物理空间单位。每个页面都有个编号叫页号，从0开始。每个内存块也有编号，从0开始。

页面大小由硬件（系统）决定，一般为2的若干次幂，有些是512B，有些是4K等，不同机器的页面大小不同。

· 分页存储如何实现地址转换（逻辑地址->物理地址）？

分页存储采用动态重定位，即装入时不进行地址转换，运行指令时才进行地址转换。指令的地址是逻辑地址。

逻辑地址转为物理地址的过程如下：

例如，程序中某个数据的逻辑地址为80，页面大小为50，页号块号映射关系为 块号数 = 页号数+10，求物理地址。

P = floor(80 / 50) = 1

i = 80 % 50 = 30

B = 1 + 10 = 11

S = 11 * 50 + 30 = 580

因此要得到逻辑地址需要得到

1、逻辑地址对应的页号P

2、逻辑地址在页内的偏移量i

3、页号在内存中的块号B（或者说页面在内存的开始地址M，M=B * p + 1）

计算机进行地址转换的方法更方便，由于OS一般会将页面大小设为2的k次幂。因此计算机得到页号P和页内地址i可以用用位运算和逻辑运算。

例如 32位的逻辑地址，页面大小为 2^12 = 4096，逻辑地址为L。

P = L >> 12

i = L & 4096

这意味着 CPU 读逻辑地址的前 20 位 就是页号，读逻辑地址的后12位就是页内偏移。当然CPU要通过位运算和逻辑运算才能做到所谓的“读前20位和后12位”。

因此得到就结论：页面大小 是 2 ^ k情况下，页号 是 逻辑地址的前 32 - k 位；页内偏移 是 逻辑地址的末尾 k 位；

· 页表

页表是系统为每个进程设立的进程页号与内存块号的映射关系表。

进程的页表保存在内存中，而页表在内存的指针存在PCB内。

需要注意：

1. 一个进程对应一张页表

2. 进程的每个页面对应一个页表项

3. 每个页表项由“页号”和“块号”组成，但页号是“隐含”的，不占存储空间，页表实际只保存了块号（页号相当于从0开始的下标）。

4. 每个页表项的长度是相同的

5. 如果不采用多级页表，则一个页表是连续存放在内存中（而非离散）。

一个页表项的大小取决于内存最多有多少个物理块。

假设某系统物理内存大小为 4GB，页面大小为 4KB，则 每个页表项至少应该为多少字节？

4GB 的内存总共会被分为 2^32 / 2^12 = 2^20个内存块

内存块号的范围应该是 0 ~ 2^20 -1

内存块号至少要用 20 bit 来表示，即至少要用3B来表示块号（3*8=24bit）

由于页号是隐含的，因此每个页表项占3B。

· 基本地址变换机构

基本地址变换机构是帮助系统将逻辑地址转换为物理地址的硬件设施。这些硬件中最重要的是页表寄存器（PTR）。

页表寄存器存放运行态进程的页表在内存中的起始地址F 和页表长度M（M是页表表项个数）。

进程未执行时，页表的始址 和 页表长度 放在进程控制块（PCB）中，当进程被调度时，操作系 统内核会把它们放到页表寄存器中。

下图为CPU将 程序计数器中的下一条指令的逻辑地址 转为指令的物理地址的过程。

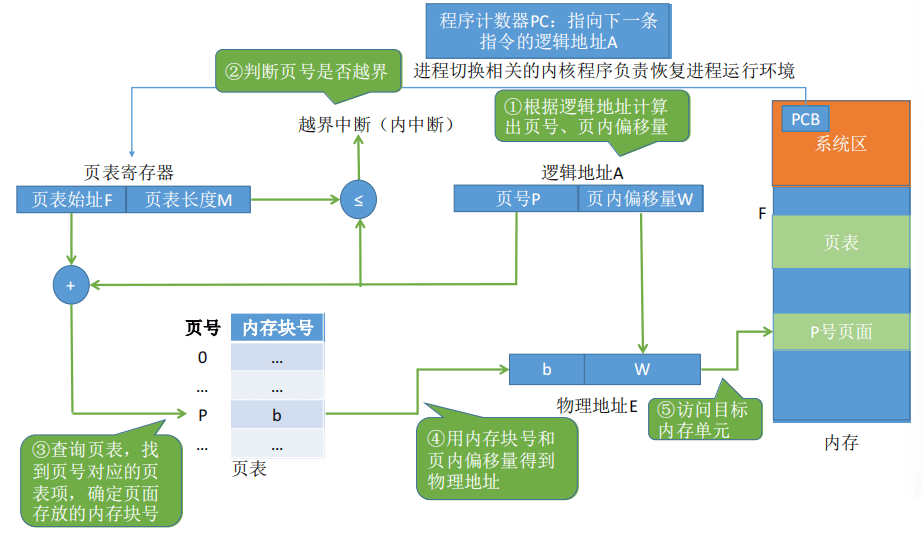
①计算页号 P 和页内偏移量W

②比较页号P 和页表长度M，若 P≥M，则产生越界中断，否则继续执行。（注意：页号是从0开 始的，而页表长度至少是1，因此 P=M 时也会越界）

③计算页号P对应的页表项地址 = 页表起始地址F + 页号P *页表项长度，取出该页表项内容b， 即为内存块号。

④计算 E = b * L + W，用得到的物理地址E 去访存。（如果内存块号、页面偏移量是用二进制表 示的，那么把二者拼接起来bW就是最终的物理地址了）

例：若页面大小L 为 1K 字节，页号2对应的内存块号 b = 8，将逻辑地址 A=2500 转换为物理地址E。

答案是E=8644。请小伙伴们自行计算。

从上面的过程中我们注意两点：

1、页式管理的地址是一维的，因为只需向系统提供一个 逻辑地址 系统就能算出物理地址。

2、CPU根据逻辑地址访问某个中的指令或数据时会发生2次内存IO，一次是根据页号+页表地址查页表，一次是实际访问目标指令或数据。

为了让CPU根据逻辑地址寻址可以更快，计算机使用快表把访问过的页表项缓存到CPU中，如果下次根据页号命中快表中的页表项，则可以减少查页表这次内存IO。

在介绍快表之前需要先介绍局部性原理。

· 局部性原理

分为时间局部性和空间局部性。

时间局部性：如果执行了程序中的某条指令，那么不久后这条指令很 有可能会再执行；如果某个数据被访问过，不久之后该数据很可能再 次被访问。（因为程序存在大量的循环）

空间局部性：一旦程序访问了某个存储单元，在不久之后，其附近的 存储单元也很有可能被访问。（因为很多数据在内存中都是连续存放的）

时间局部性强调对同一个指令或数据的重复访问。空间局部性强调对邻近指令或数据的访问。

例如下面这段代码：

int i = 0;
int a[100];
while(i < 100){
    a[i] = i;
    i++;
}

while代码块内的重复执行就是时间局部性的体现，会重复访问相同的指令和 i 这个数据；数组a的访问就是空间局部性的体现，a[0~99]是连续存储的，对a[0]~a[99]的访问很可能是访问同一个页面。

· 快表

快表（TLB）本质上是一种称为联想寄存器的硬件，用来缓存CPU最近访问过的若干个页表项，可以加快地址转换的速度。访问快表的速度远高于访问内存的速度。

根据时间和空间局部性，CPU根据逻辑地址的页号查询页表时，可能连续查到同一个页表项，因此快表正是利用了局部性原理优化了地址转换的过程。而局部行原理也可以使快表的命中率高达90%。

下图为添加了快表之后的地址变换机构。

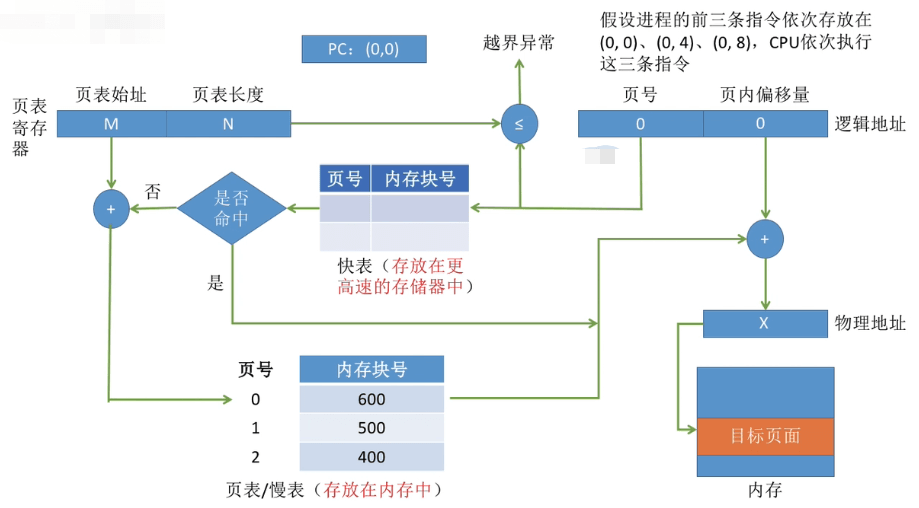
① CPU给出逻辑地址，由某个硬件算得页号、页内偏移量，将页号与快表中的所有页号进行比较（即使遍历所有页号是O(n)复杂度，但该过程快到耗时可以忽略不计，因为这是高速缓存）。

② 如果页号命中快表则从快表读出对应的块号，块号+页内偏移量拼接得到物理地址，访问该物理地址对应的内存单元。

因此， 若快表命中则访问某个逻辑地址仅需一次访存即可。

③ 如果没有命中快表，则需要访问内存中的页表，将该页表项存入快表， 以便后面可能的再次访问。但若快表已满，则必须按照一定的算法对旧的页表项进行替换。

因此， 若快表未命中，则访问某个逻辑地址需要两次访存。

· 多级页表

采用单级页表会有两个问题。

1、页表必须连续存放在内存，当页表很大时，页表需要占用多个连续的内存块。而连续存储会造成内存碎片。

对于该问题，系统采用多级页表来解决。

2、根据局部性原理，进程一段时间内可能只访问特定的几个页面，因此没有必要让整个页表常驻内存。

对于该问题，系统采用虚拟内存技术解决。

举个例子：

某32位计算机系统按字节编址，采用分页存储管理，页 面大小P为4KB，页表项长度L为 4B。请问该计算机的最长一个页表会占用多少个页面？

a. 先要知道一个页表最多会有多少字节S。S / P就是答案。

b. 要知道S，就要先知道一个页表最多有多少表项，即最大页号N。

c. 由前面的知识我们知道，逻辑地址分为前面的若干位A表示页号，后面的若干位B表示页内偏移（即页面大小的位数）。因此最大页号取决于 逻辑地址中 前面若干位的位数A。

已知页面大小是12位。

N = 2^A = 2 ^ (32-12) = 2^20

S = 4 * N = 2 ^ 22

S / P = 2^22 / 2^12 = 2^10 = 1K 个页面

每个进程的页表就可能占用连续1024个内存块。

为了解决页表需要连续占用多个物理块这个问题，操作系统使用两级页表。

操作系统将单级页表划分为多个页，每页包含若干个表项，一个单级页表被分散存储在内存不相邻的页中。

再用一个作为目录的页表记录单级页表的页号与其对应的块号，目录页表就是一个一级页表，或称为页目录表，原本的单级页表变成多个二级页表。一级页表的一个表项代表一个二级页表的位置。

如下如所示：

地址转换过程：

1、使用二级页表时，系统会将一个逻辑地址按照位数解释为3个部分：一级页号、二级页号和数据所在的页内偏移。

2、从PCB 中读出页目录表始址，再根据一级页号和页目录表始址在内存查页目录 表，找到下一级页表在内存中的存放位置。

3、根据二级页号和二级页表的始址在内存中查二级页表，找到最终想访问的内存块号。

4、根据目标内存块号 + 页内偏移得到物理地址，在内存中查找目标数据或指令。

注意两个细节：

1、对于一个更长的逻辑地址，意味着系统的页面数量上限更多，系统可能使用三级或四级页表才能实现页表离散存储。非顶级页表的个数可以有多个，但每个页表的大小不能超过一个页面；顶级页表的个数只能有一个，只占用1个页面。

根据这个原则可以判断出一个系统需要采用几级页表。

2、无论是多少级页表，进程的PCB只记录顶级页表的起始指针。因此n级页表下，CPU根据逻辑地址访问目标值需要进行 n+1 次内存访问（因为只能从顶级页表开始找起）。

例题：

某系统按字节编址，采用 40 位逻辑地址，页面大小为 4KB，页表项大小为 4B，假设采用纯页式 存储，则要采用（）级页表，页内偏移量为（）位，每级页号分别占逻辑地址的多少位？

页面大小 =4KB=2^12B，按字节编址，因此页内偏移量为12位

页号 =40 - 12 =28 位

页面大小 =2^12B，页表项大小 =4B ，则每个页面可存放 2^12/4 =2^10个页表项。

如果用单级页表，该页表有2^28个表项，需要用 2^18 个连续页面存储。不符合顶级页表占有页面个数只有1个的原则。

如果用两级页表，第二级页表用 2^18 个离散页面存储，顶级页表（页目录表）有 2^18个表项，要用2^18/2^10 = 2^8个页面存储页目录表。不符合顶级页表占有页面个数只有1个的原则。

如果采用三级页表，底层页表用2^18个离散页面存储，二级页表用2^8个离散页面存储，顶级页表只有2^8个表项，用一个页面存储即可。因此采用三级页表，一级、二级、三级页号占逻辑地址的 8，10，10位。

如果做这种题熟练的同学，直接用 ceil(28 / 10) = 3 得出要采用三级页表。

· 页式存储下的内部碎片

考虑一种情况，系统的页面大小是4K，一个进程大小为49K，会占用13个页面，但是最后一个页面只用了1K，剩余3K没有被该进程使用，也不会不能被其他进程使用，于是会造成3K的内存碎片。

因此页式存储不会产生外部碎片，但会产生内部碎片，而且每个进程产生的碎片大小范围为 0~页面大小p，可以认为每个进程平均产生 p/2 字节的内部碎片大小。

· 页面尺寸

页面尺寸是影响分页管理中内存使用效率的重要因素。

如果页面尺寸太大，就会出现越大的内存碎片（因为每个进程平均有半个页面或内部块会成为碎片）；如果页面太小，那么内存的块号上限也越大，同一个进程所需的页面数也越多，该进程对应的页表中的表项也越多，这个页表占用的空间越多，一方面会额外的占用内存，另一方面会造成多级页表，每多一级页表，CPU根据逻辑地址找到目标值就需要多一次内存IO。

假设进程平均大小为 s 字节，页面尺寸 p 字节，每个页表项（一行）占e字节。则每个进程需要页面数为 s/p 字节，页表的存储要占 se/p 字节，每个进程的内部碎片平均为 p/2。因此页表和内部碎片带来的总内存开销为：se/p + p/2。

而这个公式也证明了页面尺寸p不能太大也不能太小，否则带来的内存开销都会较大。公式求导得到 p = 根号下(2se)，此时的p是最佳的p。

更多内容请关注微信公众号