请关注公众号


树
树是一种非线性的数据结构,树包含根,枝,叶
树的特征:
1.树是有层次的:越接近顶层的分类越普遍,越接近底层的分类越独特
2.一个节点的子节点和另一个节点的子节点相互之间是隔离,独立的
3.每一个叶节点(最底层的节点)都具有唯一性
树的应用:
文件系统
HTML标签
域名体系
树结构的术语:
Node 节点:每个节点都有一个key-value
Edge 边:边是连接两个节点的线,表示节点之间有关系,边有出入方向,一个节点可以有一条入边(父节点连向自己的边),有多条出边。根节点没有入边,叶节点没有出边
Root 根(节点) 树中唯一没有入边的节点
Path 路径:由边依次连接在一起的节点的有序列表
Children 子节点
Parent 父节点
Sibling 兄弟节点:具有同一个父节点的节点
Subtree 字数
Left 叶节点:底层节点
Level 层级:从根节点开始到某一个节点所经过的边数。根节点的层级是0层
高度:最大层级即高度
树其实是节点和边的集合
==========================================
树的python实现
1.用列表+递归实现一个二叉树(二叉树是一个父节点最多只能有两个子节点的树)
思路:一个列表存放3个元素,第一个元素是根节点,第二个和第三个元素是左子树和右子树,左子树和右子树又包含了分支节点。
为什么用递归实现,因为树的局部结构和整体结构是相似的,这种情况就很适合使用递归实现。例如左子树的结构和整棵树一样都是二叉树,左子树的左子树也是一个二叉树。
# 使用列表实现一个二叉树
class BinaryTree:
def __init__(self,root):
# 第二和第三个元素是左子树和右子树,如果要实现n叉树,则需要列表有n+1个元素
self.tree = [root,[],[]] # root是根节点,是一个普通类型的数据而不是列表
# 添加一个新节点到树中作为其直接的左子节点
def insertLeft(self,item,tree=[]): # item是一个普通类型的数据
tree = tree if tree else self.tree
leftTree = tree.pop(1)
if len(leftTree) > 0:
tree.insert(1,[item,leftTree,[]])
else:
tree.insert(1,[item,[],[]])
# 添加一个新节点到树中作为其直接的右子节点
def insertRight(self,item,tree=[]):
tree = tree if tree else self.tree
rightTree = tree.pop(2)
if len(rightTree) > 0:
tree.insert(2, [item, [], rightTree])
else:
tree.insert(2, [item, [], []])
# 获取根节点
def getRootVal(self,tree=[]):
tree = tree if tree else self.tree
return tree[0]
# 设置根节点
def setRootVal(self,item,tree=[]):
tree = tree if tree else self.tree
tree[0] = item
# 获取一个树的左子树
def getLeftChild(self,tree=[]):
tree = tree if tree else self.tree
return tree[1]
# 获取一个树的右子树
def getRightChild(self,tree=[]):
tree = tree if tree else self.tree
return tree[2]
def __str__(self):
return str(self.tree)
if __name__ == "__main__":
t = BinaryTree(1)
t.insertLeft(4)
t.insertLeft(5)
t.insertRight(6)
t.insertRight(7)
print(t)
l = t.getLeftChild()
print(l)
t.setRootVal(9,l)
print(t)
t.insertLeft(11,l)
print(t)
print(t.getRightChild(t.getRightChild()))
从上面的代码可以看出,添加节点的时候并非只能从叶节点添加节点,也可以从任意一个非叶节点下添加一个节点。
2.使用链表实现二叉树
# 使用链表实现二叉树
class Node: # 链表节点类,这个节点类和之前单向链表或者双向链表中的节点类不同,不同在于它的有两个指针,因为二叉树的一个节点有两条边
def __init__(self,value):
self.value = value
self.left = None # 左指针
self.right = None # 右指针
def __str__(self):
return str({"value":self.value,"left":self.left,"right":self.right})
class LinkedListBinaryTree(Node): # 二叉树本质是一个有两个指针的节点
# 往一棵树的根节点下插入一个左子节点
def insertLeft(self,nodeValue):
leftTree = LinkedListBinaryTree(nodeValue) # 生成一棵左子树
if self.left == None:
self.left = leftTree
else:
leftTree.left = self.left
self.left = leftTree
def insertRight(self, nodeValue):
rightTree = LinkedListBinaryTree(nodeValue) # 生成一棵左子树
if self.right == None:
self.right = rightTree
else:
rightTree.right = self.right
self.right = rightTree
def getRootVal(self): # 获取根节点的值
return self.value
def setRootVal(self,value):
self.value = value
def getLeftChild(self): # 获取左子树
return self.left
def getRightChild(self):
return self.right
使用链表实现树更加的直观
=========================================
树的应用:表达式解析
# 简单的数学表达式解析(用二叉树实现)
class MathExpression:
num = list("0123456789")
opDict = {"+": operator.add, "-": operator.sub, "*": operator.mul, "/": operator.truediv}
def __init__(self,expression):
self.expression = list(expression) # 传入的表达式是一个全括号表达式,每一个操作都用()包住
self.currentTree = None # 记录当前子树是哪一棵
self.topTree = None # 记录最顶层的子树
self.degree = [] # 将经过树的层用存入到栈内(目的是让currentTree可以回到上一层子树),栈用列表模拟
# 构建一棵表达式解析树
# 这棵树是由多个单层的二叉树构建而成的一棵大二叉树
# 叶子节点只能是操作数,非叶子节点和根节点只能是操作符
# 当遇到最后一个“)”的时候,当前子树 currentTree 会回到底层
def build(self):
for item in self.expression:
if item == " ":
continue
if item == "(": # 遇到左括号则创建一棵单层的二叉子树
if self.currentTree == None: # 如果没有创建过树,则该二叉子树作为顶层的树干
self.currentTree = LinkedListBinaryTree()
self.topTree = self.currentTree
else: # 如果已经有了顶层的树干,则创建的二叉子树添加为当前子树的左子树或者右子树
if self.currentTree.left == None:
self.currentTree.insertLeft("")
tree = self.currentTree.getLeftChild()
else:
self.currentTree.insertRight("")
tree = self.currentTree.getRightChild()
self.degree.append(self.currentTree) # 进入下一层之前,先记录这一层是哪一个分支
self.currentTree = tree # 进入下一层
if item == ")": # 遇到右括号则返回到当前子树的上一层子树
if len(self.degree) != 0:
lastDegree = self.degree.pop()
self.currentTree = lastDegree
if item in self.opDict: # 遇到操作符则为当前子树的根节点设置值
self.currentTree.setRootVal(item)
if item in self.num: # 遇到操作数则将操作数记录到当前子树的左叶子节点或者右叶子节点
if self.currentTree.left == None:
self.currentTree.left = item
else:
self.currentTree.right = item
# 计算表达式树中表达式的结果(使用递归 + 分治策略)
def calculate(self):
# 这个不是结束条件而是一种特殊情况的判断
if self.currentTree.getRootVal() not in self.opDict:
return self.currentTree.getRootVal()
op = self.opDict[self.currentTree.getRootVal()]
if not isinstance(self.currentTree.left, LinkedListBinaryTree): # 结束条件
left = self.currentTree.left
else:
self.degree.append(self.currentTree)
self.currentTree = self.currentTree.left
left = self.calculate()
if not isinstance(self.currentTree.right, LinkedListBinaryTree): # 结束条件
right = self.currentTree.right
else:
self.degree.append(self.currentTree)
self.currentTree = self.currentTree.right
right = self.calculate()
res = op(int(left),int(right))
self.currentTree.setRootVal(res) # 没有这一步也可以
self.currentTree = self.degree.pop() # 每计算出一个子树的值就返回上一层
return res
if __name__ == "__main__":
expression = "((1+(2*3))-4)"
mp = MathExpression(expression)
mp.build() # 构建表达式树
print(mp.currentTree == mp.topTree) # 当构建完表达式树的时候,当前节点变回根节点
print(mp.calculate())
树的遍历
有3种方法
1.前序遍历(preorder)
先访问根节点,再递归的前序访问左子树,最后前序访问右子树
2.中序遍历(inorder)
先递归的中序访问左子树,在访问根节点,最后中序的访问有节点
3.后序遍历(postorder)
先后序的访问左子树,再后序号的访问右子树,最后访问根节点
接下来分别实现这3种遍历方法
# 树的遍历
# 前序遍历(以从上到下的顺序遍历)
def preorder(binaryTree):
if isinstance(binaryTree,LinkedListBinaryTree):
print(binaryTree.getRootVal())
preorder(binaryTree.getLeftChild())
preorder(binaryTree.getRightChild())
elif binaryTree != None:
print(binaryTree)
# 中序遍历(以从左到右的顺序遍历)
def inorder(binaryTree):
if isinstance(binaryTree,LinkedListBinaryTree):
inorder(binaryTree.getLeftChild())
print(binaryTree.getRootVal())
inorder(binaryTree.getRightChild())
elif binaryTree != None:
print(binaryTree)
# 后序遍历(以从下到上的顺序遍历)
def postorder(binaryTree):
if isinstance(binaryTree,LinkedListBinaryTree):
postorder(binaryTree.getLeftChild())
postorder(binaryTree.getRightChild())
print(binaryTree.getRootVal())
elif binaryTree != None:
print(binaryTree)
if __name__ == "__main__":
expression = "((1+(2*3))-4)"
mp = MathExpression(expression)
mp.build() # 构建表达式树
preorder(mp.topTree)
print("---")
inorder(mp.topTree)
print("---")
postorder(mp.topTree)
从上面的代码可以看出,三种遍历方式代码完全一样,只是调用顺序有所不同。
口诀
前序:上左右
中序:左上右
后序:左右上
这里值得一提的是,无论是哪种遍历都是用了分治策略。
上面的表达式树在calculate的时候是先获取子树的根节点,再获取左子节点,再获取右子节点,是一个上左右的顺序,所以属于前序遍历。
下面写一个函数版本的表达式树的构建,解析和遍历# 函数版的表达式树
def buildParseTree(fexp):
fexp = list(fexp)
# 一开始先创建一个顶层子树,根节点不赋值
currentTree = None
stack = [] # 用栈保存currentTree经过的哪几层子树,方便当前树currentTree的回溯
for i in fexp:
# print(stack)
if fexp == " ":
continue
if i == "(":
if currentTree == None:
currentTree = LinkedListBinaryTree("")
currentTree.insertLeft("") # 创建一棵左子树
currentTree.insertRight("") # 创建一棵右子树
stack.append(currentTree) # 进入下一层的树前,先将本层的树放入stack中,记录currentTree经过的树
currentTree = currentTree.getLeftChild() # 进入下一层树
# print(currentTree)
elif i not in ["(","+","-","*","/",")"]:
# print(currentTree)
currentTree.setRootVal(i)
currentTree = stack.pop()
elif i in ["+","-","*","/"]:
currentTree.setRootVal(i)
stack.append(currentTree)
currentTree = currentTree.getRightChild()
elif i == ")":
if len(stack):
currentTree = stack.pop()
return currentTree
# 使用中序遍历的方式计算
def calculateParseTree(tree):
opDict = {"+": operator.add, "-": operator.sub, "*": operator.mul, "/": operator.truediv}
if tree.getRootVal() not in ["+","-","*","/"]: # 如果根节点的值是数值而不是符号,则满足结束条件
return tree.getRootVal()
left = calculateParseTree(tree.getLeftChild())
op = opDict[tree.getRootVal()]
right = calculateParseTree(tree.getRightChild())
return op(int(left),int(right))
if __name__ == "__main__":
expression = "((1+(2*3))-4)"
mp = buildParseTree(expression)
inorder(mp)
print(calculateParseTree(mp))
calculateParseTree这个方法使用了中序遍历的方式去计算表达式树的值。
优先队列
队列是先进先出的(FIFO),优先队列是队列的一种变体,也是先进先出,但是允许一些关键的任务或者指定的任务优先插到队首或者队尾弹出。
举一个例子,往优先队列里面插入
5,7,3,11
数值小的优先级更大,我希望弹出的时候优先级大的会先弹出来
所以弹出来的结果是
3,5,7,11
要实现这个功能,可以使用排序来做,每次插入一个数的时候将这个数和队列中其他的数进行比较,并将这个数插入到合适的位置。
如果使用有序表(即通过排序的方式)实现这个优先队列,弹出的时候复杂度是O(1),插入的时候复杂度是O(n)
接下来介绍使用二叉堆实现优先队列,可以达到弹出和插入的复杂度都是O(logn)
为了使堆操作能保持在对数水平上,就必须采用二叉树结构而且必须始终保持二叉树的“平衡”,即树根左右子树拥有相同数量的节点(对称);
我们采用“完全二叉树”的结构来近似实现“平衡”
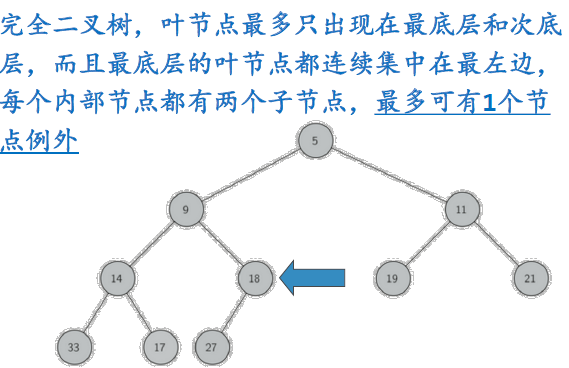
完全二叉树,叶节点最多只出现在最底层和次底层,而且最底层的叶节点都连续集中在最左边,每个非叶节点都有两个子节点,最多可有1个节点例外
完全二叉树可以用一个非嵌套的列表来表示(就是一个一维的列表)。这棵二叉树从逻辑上来说是一棵树,但是具体表现出来的却是一个列表,所以我们将他叫做二叉堆(用列表表示一个堆)。
这个二叉堆的特性如下:
假设某一个节点的下标为p,那么其左子节点的下标为2p,右子节点下标为2p+1,父节点下标为 p//2(向下取整)
树节点的下标就是列表的下标,节点的值就是列表的值
整个列表记录的节点的顺序是记录着树的从上到下从左到右的顺序。
符合“堆”性质的二叉树,父节点的值总是比子节点的值小,叶子节点的值则最大。也就是说,上面的节点的值比下面节点的值要小,因此任何一条路径都是一个已排好序的数列。但是同一层中,左边节点的值比右边节点的值可大可小(上面的节点比下面的节点值小,但左边的节点不一定比右边的节点小)。
.png)
具体思路:
构建一个二叉堆类,这个二叉堆就是优先队列,这个类有三个主要方法:insert,pop和buildHeap
insert 往优先队列尾部插入数据
插入之后,该方法内部会将数据调整到合适的位置使得该数据所在的下标满足上面设定的条件
例如 插入的是一个较小的数,但是由于上面规定了子节点的值比父节点的大,所以这个数的在树节点中应该要“上浮”到某一个节点以满足上面的条件
该算法相当于是冒泡排序1次,但是只是对树中的某一条路径排序而不是对整个二叉堆列表的元素排,所以复杂度为 O(logn)
.png)
.png)
pop 从优先队列头部弹出优先级最高的元素(就是值最小的元素,也就是根节点)
当弹出根节点之后,根节点应该补上其他节点。
我们选择将二叉堆列表中最后一个元素(最后一个叶节点)调到根节点,但是这个元素肯定比下面的各个子节点大,所以要将该跟节点“下沉”到合适的位置。
该函数复杂度也是O(logn)
.png)
.png)
.png)
buildHeap 构建一个二叉堆
就是将一个乱序的列表构建成二叉堆列表,构建的思路就是对非叶子节点的节点从下到上逐一进行下沉,由于下沉的复杂度是 O(logn),需要对n-k个节点进行下沉(其中k是叶节点个数),所以buidHeap的复杂度是 O(nlogn)
.png)
# 二叉堆实现优先队列
class BinaryHeap:
def __init__(self):
self.heapList = [0] # 用一个不嵌套的列表表示二叉堆(优先队列);将第一个元素设为0的目的是为了让根节点从下标1开始,这样就可以满足“某一个节点的下标为p,那么其左子节点的下标为2p,右子节点下标为2p+1,父节点下标为 p//2”这个条件;所以第一个元素0只是为了占位
self.currentSize = 0 # 记录树节点个数,它既是节点个数,也是最后一个节点的下标
# 往优先队列尾部插入
def insert(self,item):
self.heapList.append(item)
self.currentSize += 1
# 元素插入尾部后做数据上浮
self.__percUp()
# 从优先队列头部弹出元素
def pop(self):
minVal = self.heapList[1] # 这里不要用pop(1)然后再用insert(1,self.heapList[-1]),因为这两个都是O(n)的复杂度
self.heapList[1] = self.heapList[-1]
self.heapList.pop()
self.currentSize -= 1
# 尾部元素补上根节点后做根节点下沉
self.__percDown(1) # 传入的1是根节点下标,表示要下沉根节点
return minVal
# 传入一个无序的列表,根据这个列表构建出一个二叉堆
def buildHeap(self,alist):
self.heapList = [0] + alist[:]
self.currentSize = len(self.heapList)-1
# 构建的思路就是对非叶子节点的节点从下到上逐一进行下沉操作
i = self.currentSize // 2 # 这个i下标就是第一个进行下沉操作的下标,也是所有要下沉操作的节点中最后一个节点
while i>0:
self.__percDown(i)
i-=1
# 上浮最后一个尾部节点
# 上浮的思路就是将最后一个节点和所有祖先节点的值进行比较,如果该节点比某一个祖先节点小则和它互换
def __percUp(self):
i = self.currentSize # 最后一个元素的下标
while i // 2 > 0: # i//2是下标为i的节点的父节点的下标
fatherIndex = i//2
if self.heapList[fatherIndex] > self.heapList[i]:
self.heapList[fatherIndex],self.heapList[i] = self.heapList[i],self.heapList[fatherIndex]
i = fatherIndex
else:
break
# 下沉节点,index是要下沉的节点的下标
def __percDown(self,index):
# 先比较index节点下左右子节点哪个大,然后再拿左右子节点中小的那个节点和index节点比
# 如果index节点比它大,就和这个子节点交换
# 例如 index节点的值是 100 它的左子节点是99,右子节点是98,那么index节点要和它的右子节点互换,这样父节点就变成了98,比左子节点99小,符合父节点比子节点小的这个规则
stoped = False
while index*2 <= self.currentSize and not stoped: # index*2是左子节点的下标,index*2 <= self.currentSize表示存在index节点的左子节点。如果当前节点没有左子节点,那么右子节点肯定也没有,此时下沉停止
# print(index)
leftIndex = index*2
rightIndex = index*2 + 1
if rightIndex > self.currentSize: # 如果没有右子节点但是有左子节点,那么就拿左子节点和index节点比较
comparedIndex = leftIndex
else:
comparedIndex = leftIndex if self.heapList[leftIndex] <= self.heapList[rightIndex] else rightIndex
if self.heapList[index] > self.heapList[comparedIndex]: # 如果index节点比要比较的节点的值大则互换,否则不互换
self.heapList[index],self.heapList[comparedIndex] = self.heapList[comparedIndex],self.heapList[index]
index = comparedIndex
else: # 如果index节点比要比较的子节点的值小,说明可以无需继续下沉了,停止循环
stoped = True
if __name__ == "__main__":
bh = BinaryHeap()
bh.insert(10)
bh.insert(100)
bh.insert(1)
bh.insert(22)
bh.insert(53)
bh.insert(34)
bh.insert(54)
bh.insert(23)
bh.insert(11)
bh.insert(17)
bh.insert(87)
print(bh.heapList)
while bh.currentSize>0:
print(bh.pop())
alist = [10,100,1,22,53,34,54,23,11,17,87]
bh2 = BinaryHeap()
bh2.buildHeap(alist)
while bh2.currentSize>0:
print(bh2.pop())
使用二叉树实现查找
使用二叉树进行查找的数叫做“二叉查找树”(BST)
回想一下,之前我们用过两种方式实现查找
1.有序表+二分查找
2.散列表+散列函数
加上这里的二叉树查找就是3种方式
用1句话概括这个二叉查找树:比父节点小的数都在左子树,比父节点大的数都在右子树
换句话说:节点A左边的所有子树和分支的值都比A的值小,节点A右边的所有子树和分支的值都比A的值大
具体实现:
首先这个二叉查找树使用链表结构实现。二叉查找树本身就是一个链表,这个链表的节点TreeNode有如下特性:
节点有三个指向:left 指向左子节点;right 指向右子节点;parent 指向父节点
节点可以存储key和value两个属性,表示这个节点包含的内容。
比较大小是指比较key的大小而不是value的大小。
# coding=utf-8
# 二叉查找树的节点
class TreeNode:
def __init__(self,key,value,left=None,right=None,parent=None):
self.key = key
self.value = value
self.left = left
self.right = right
self.parent = parent
# 判断是否有左子节点
def hasLeftChild(self):
return self.left
# 判断是否有左子节点
def hasRightChild(self):
return self.right
# 判断是否是左子节点
def isLeftChild(self):
return self.parent and self.parent.left == self
# 判断是否是右子节点
def isRightChild(self):
return self.parent and self.parent.right == self
# 判断是否为根节点
def isRoot(self):
return not self.parent
# 判断是否为叶子节点
def isLeaf(self):
return (not self.left) and (not self.right)
# 判断是否有子节点
def hasAnyChild(self):
return self.left or self.right
# 判断是否两个子节点都有
def hasBothChild(self):
return self.left and self.right
# 替换节点(用于删除根节点时调用并用根节点的左子节点或者右子节点替换自己)
def replaceNode(self,key,value,lc,rc):
self.key = key
self.value = value
self.left = lc
self.right = rc
if self.hasLeftChild():
self.left.parent = self
if self.hasRightChild():
self.right.parent = self
def findSuccessor(self):
node = self
while node.hasLeftChild():
node = node.left
return node
# 将后继节点从原位置挖出
def spliceOut(self):
if self.isRightChild():
self.parent.right = None
else:
if self.hasRightChild():
self.parent.left = self.right
self.right.parent = self.parent
elif self.isLeaf():
self.parent.left = None
# 后继节点不会有左节点 无需判断 if self.hasLeftChild()
# 使用中序遍历作为迭代方法
def __iter__(self):
if self.hasLeftChild():
for elem in self.left: # 用for对self.left遍历的时候又会调用 self.left 的__iter__ 所以相当于是对__iter__()进行递归调用
yield elem
yield self.key
if self.hasRightChild():
for elem in self.right:
yield elem
# 二叉查找树
class BST: # BinarySearchTree
def __init__(self):
self.root = None # root是BST的根节点
self.size = 0
# 往BST中添加节点,添加节点的规则要满足key如果大于父节点的key则作为其右子节点,如果小于父节点的key则作为其左子节点
def put(self,key,value):
if self.root:
self.__put(self.root,key,value)
else:
self.root = TreeNode(key,value)
self.size += 1
def __put(self,currentNode,key,value):
if key < currentNode.key: # 如果要插入的key小于目前节点的key,则这个key就放在currentNode的左节点
if currentNode.hasLeftChild():
self.__put(currentNode.left,key,value) # 如果这个节点已经有左节点,则递归
else: # 如果没有左子节点则创建左子节点,并且currentNode的left要指向这个节点,而新生成的这个节点的parent要指向currentNode
currentNode.left = TreeNode(key,value,parent=currentNode)
else: # 如果要插入的key大于目前节点的key,则这个key就放在currentNode的右节点
if currentNode.hasRightChild():
self.__put(currentNode.right, key, value)
else:
currentNode.right = TreeNode(key,value,parent=currentNode)
def get(self,key):
if self.root:
res = self.__get(self.root,key) # 返回的res可能是none,也可能是一个节点
return res and res.value
else:
return None
def __get(self,currentNode,key):
if currentNode == None: # 说明找不到key
return None
if currentNode.key == key:
return currentNode
elif currentNode.key > key:
return self.__get(currentNode.left,key)
else:
return self.__get(currentNode.right,key)
# 根据key删除某个节点A
# 分为三种情况:1. 节点A没有子节点; 2. 节点A只有1个子节点; 3. 节点A有两个子节点
def remove(self,key):
# 先获取key所在的节点
node = self.__get(self.root,key)
if node.isLeaf(): # 1. 节点A没有子节点
if node.parent.left == node:
node.parent.left = None
else:
node.parent.right = None
node.parent = None
elif node.hasAnyChild() and not node.hasBothChild(): # 2. 节点A只有1个子节点
sonNode = node.left if node.hasLeftChild() else node.right
if node.isLeftChild():
node.parent.left = sonNode
elif node.isRightChild():
node.parent.right = sonNode
else: # 要删除的节点是根节点
self.root = sonNode
sonNode.parent = None
else: # 3. 节点A有两个子节点
# 这种情况需要找到节点A右边所有节点中key最小的子孙节点,并用该子孙节点替换节点A。这么一来,节点A这个位置还是符合左边的节点比A节点的key小,右边的节点比A节点的key大
# 这里说一下后继节点succ的特点:succ不会有左子节点;succ本身只能是左节点
succ = node.right.findSuccessor() # 找到后继节点,后继节点succ是不会有左子节点的,原因很简单你自己想想吧
succ.spliceOut() # 将后继节点从原本的位置挖出来
node.key = succ.key # 最后用后继节点替换要被删的节点,一旦替换那么原node就算被删除
node.value = succ.value
def __setitem__(self, key, value):
self.put(key,value)
def __getitem__(self, key):
return self.get(key)
def __contains__(self, key):
if self.get(key):
return True
else:
return False
def __len__(self):
return self.size
def __iter__(self):
if self.root:
return self.root.__iter__()
if __name__ == "__main__":
# import random
# dataKey = [i for i in range(1,50,3)]
# random.shuffle(dataKey)
dataKey = [34, 43, 49, 25, 46, 13, 1, 22, 40, 31, 7, 19, 37, 16, 4, 28, 10]
print(dataKey)
bst = BST()
for i in dataKey:
bst.put(i,i/2)
for i in bst:
print(i,bst[i])
print(bst.get(40))
print(bst.get(25))
print(bst.get(22))
print(bst.get(33))
print("===================================")
bst.remove(40)
bst.remove(22)
bst.remove(25)
bst.remove(28)
for i in bst:
print(i,bst[i])
put方法性能平均为 O(logn)
get方法也是O(logn)
最复杂的remove方法要分三种情况
a. 要删除的节点没有子节点
.png)
b. 要删除的节点有1个子节点
.png)
c. 要删除的节点有2个子节点
.png)
remove方法的复杂度主要体现在寻找被删除的节点和寻找后继节点,使用到了_get()方法,这个过程的复杂度是 O(logn), 而删除的过程则是简单的指针赋值,复杂度是O(1)。所以remove方法的复杂度也是 O(logn)
AVL 平衡树
对于上面的BTS二叉树,考虑一种情况,假如有一串数据,它的key是1~10,value是1~10的平方。
假如我按照key的顺序往BST添加节点会出现一个现象:
这棵BST树的只有右子树没有左子树,这样就相当于变成了一个双向链表。
.png)
此时put和get方法的性能都是O(n)
这个时候,二叉查找树的性能变得和有序链表一样。
此时可以使用AVL平衡树解决这个问题:
AVL平衡树是在BST的基础上添加了一个特性。这个特性具体是:保持整棵树左右两边的层数基本相同。
AVL树的平衡特性可以很好的解决上面说的这个BST顺序插入节点导致性能变差的问题。
AVL树的平衡特性使得树左右两边的层数相同因此它的put和get方法性能最差都是O(logn)
如何实现AVL树的平衡特性?
需要在每个节点记录其“平衡因子”。
这个平衡因子是一个整数,是左右子树高度差。如果某个节点的平衡因子>0则表示该节点下左边子孙节点的层数大于右边的层数。反之亦然。
一个BST中每个节点的平衡因子都在-1,0,1之间则称这种BST为平衡树(AVL)
例如有一个线性的二叉平衡树,这个树就是上面所说的顺序插入。假如是按顺序插入的key为1 2 3
那么这个BST的结构为:
1 (-2)
|
---
| |
None 2 (-1)
|
---
| |
None 3 (0)
上面的()中记录的就是平衡因子。
比如,根节点右边有两层,左边有0层,所以根节点的平衡因子 = 0-2 = -2
这个时候怎么调节平衡呢?很简单,只需要将2作为根节点,1作为2的左子节点即可。这个过程是对1进行左旋,会变成:
2 (0)
|
---
| |
1 3
考虑一种复杂点的情况
10 (-2)
|
---
| |
5 20 (-1)
|
---
| |
25 30 (-1)
|
---
| |
None 40 (0)
这种情况怎么将他变成平衡的呢?(只需让绝对值超过1的平衡因子调整为1以内即可,所以现在要将10这个根节点的平衡因子变为-1即可)
此时有两种做法:
1.将20晋升为根节点,10这个节点顺着20这个节点的左边一直降到底即可
此时变成:
20 (0)
|
-------
| |
(2)25 30 (0)
| |
--- ---
| | | |
(1)10 None None 40 (0)
|
---
| |
(0)5 None
这种做法的话 20的平衡因子变成了0,但是25的平衡因子有变成了2
2.将10作为20的左子节点,25作为10的右子节点
20 (0)
|
-------
| |
10 30 (0)
| |
--- ---
| | | |
5 25 None 40 (0)
正确的做法应该是法2
这个过程就是对10的一个左旋
有一种比较特殊的情况:
10 (-2)
|
---
| |
None 20 (1)
|
---
| |
15 None
假如按照上面的方法去做左旋的调节,会变成:
20 (2)
|
---
| |
10 None
|
---
| |
None 15
所以如果遇到这种情况,应该20这个节点进行右旋,变成
10 (-2)
|
---
| |
None 15 (-1)
|
---
| |
None 20
再对10进行左旋:
15
|
---
| |
10 20
这种情况称之为“之”型子树
PS:以上所有调整的过程,都是在往树里面添加完节点之后才开始的。
一个节点A的右边层数大于左边称之为右重;反之是左重
节点A右重则需要对节点A进行左旋;节点A左重则需要对节点A进行右旋;
