图 Graph

图的术语：
1.顶点 Node
是图的基本组成部分，顶点具有名称标识Key，也可以携带数据项value

2.边Edge（也称“弧Arc”）
作为2个顶点之间关系的表示，边连接两个顶点；
边可以是无向或者有向的，相应的图称作“无向图”和“有向图”

3.权重Weight
为了表达从一个顶点到另一个顶点的“代价”，可以给边赋权；例如公交网络中两个站点之间的“距离”、“通行时间”和“票价”都可以作为权重。

一个图G可以定义为G=(V, E)（也就是说，图就是顶点和边的集合）
其中V是顶点的集合，E是边的集合，E中的每条
边e=(v, w)，v和w都是V中的顶点；
如果是赋权图，则可以在e中添加权重分量

例如一个图有三个顶点 v1,v2,v3，其中v1和v2相连，v2和v3相连，v3和v1相连。方向是v1-->v2-->v3-->v1
那么这个图可以表示为三个公式：
G = (V,E)       # 图表示为顶点和边的集合，V是顶点，E是边
V = {v1,v2,v3}  # 顶点集合
E = {(v1,v2),(v2,v3),(v3,v1)}   # 边的集合 

其中E 中每一条边都是用两个顶点表示的。

4.路径Path
图中的路径，是由边依次连接起来的顶点序列；
无权路径的长度为边的数量；带权路径的长度为
所有边权重的和；

5.圈Cycle
圈是首尾顶点相同的路径，如下图中

(v5,v2,v3,v5)是一个圈
如果有向图中不存在任何圈，则称作“有向无圈
图directed acyclic graph: DAG”
后面我们可以看到如果一个问题能表示成DAG，就可以用图算法很好地解决。

树就是一个有向无圈图

==============================================
使用python实现一个Graph

Graph的实现有两种形式：
 

1.邻接矩阵
假如有一个图是由5个顶点构成的。那么需要构建一个6*6的矩阵。如果某个点Vx和另一个点Vy是相连接的那么矩阵中 (Vx,Vy)这个点应该填1（没有权重则填1）或者填边的权重，用于表示说Vx和Vy之间是有边的是相连的。

例如：

这就是一个
G = {V,E}
V = {v0,v1,v2,v3,v4,v5}
E = {(v0,v5,2),(v0,v1,5),(v1,v2,4),(v2,v3,9),(v3,v4,7),(v3,v5,3),(v4,v0,1),(v5,v2,1),(v5,v4,8)}
的图

该方法的优点：
简单

缺点：
如果图的边数很少，矩阵中的单元格就会有很多空白，成为“稀疏矩阵”。此时效率会很低下，浪费存储空间
在实际应用当中，大多数问题的图都是稀疏的。

所以提出一种更加有效率的方法——邻接列表。

2.邻接列表
首先维护一个字典表dictV,dictV的索引表示为所有顶点的key或者说id，dictV的值用于存储一个与自身顶点相连的顶点的字典dictRelation

例如一个图中有v1~v5这5个顶点。
dictV = {
    v1:{xxx},   # {xxx}就是dictRelation
    v2:{xxx},
    v3:{xxx},
    v4:{xxx},
    v5:{xxx}
}
v1和v3,v4相连（方向是v1指向v3和v1指向v4）,而且这两条边的权重是2和6。那么v1的dictRelation为：{v3:2,v4:6}
v3和v5相连，边权重是8，那么v3的dictRelation为：{v5:8}

可能会有人问v1和v3相连，为什么v3的dictRelation为：{v5:8}而不是{v1:2,v5:8}呢？
因为图的边是单向的，一个顶点的dictRelation只记录该顶点指向的顶点的边，不记录被谁指向的顶点的边。
 

接下来使用邻接列表的方式实现图：

# coding = utf-8

# 顶点类
class Vertex:
    def __init__(self,key):
        self.key = key
        self.connect = {}   # 存储该节点所连接的节点，下标是Vertex节点对象，值是边的权重

    # 连接一个顶点
    def connectTo(self,nbr,weight=0):   # key是所连接的顶点的key
        self.connect[nbr] = weight

    def __str__(self):
        return str(self.key) + ' connect to ' + str([x.key for x in self.connect])

    # 获取所有本顶点连接的顶点（对象）
    def getConnections(self):
        return self.connect.keys()

    # 获取本顶点的key
    def getKey(self):
        return self.key

    # 获取本顶点和某一顶点所连接的边的权重
    def getWeight(self,nbr):
        return self.connect[nbr]


# 图
class Graph:
    def __init__(self):
        self.vertList = {}      # 用于存放本图中所有的顶点,vertList的key是vertex顶点类的key，value是vertex顶点对象本身，一个顶点对象代表一个顶点
        self.vertNum = 0        # 本图中顶点个数

    # 向图中添加一个顶点
    def addVertex(self,key):
        self.vertNum += 1
        newVertex = Vertex(key)
        self.vertList[key] = newVertex
        return newVertex

    # 从图中获取某一个顶点
    def getVertex(self,key):
        if key in self.vertList:
            return self.vertList[key]
        else:
            return None

    def __contains__(self, key):
        return key in self.vertList

    # 为图中某两个顶点之间添加一条边，边是有方向的，是从from到to的
    def addEdge(self,f,t,cost): # cost就是边的权重,f和t是顶点的key
        if f not in self.vertList:
            nv = self.addVertex(f)

        if t not in self.vertList:
            nv = self.addVertex(t)

        self.vertList[f].connectTo(self.vertList[t],cost)

    # 获取图中所有顶点的key
    def getVertices(self):
        return self.vertList.keys()

    def __iter__(self):
        return iter(self.vertList.values())

 

==============================================

图的应用

1.词梯问题
词梯问题就是给你一堆的长度相同的单词，我要把一个单词 fool 变成 sage，每次只能替换1个字母，我要找到最短的单词变换序列。
例如：
给出一堆的4个长度的单词：
fool foul foil fail fall pall pole poll pool cool pope pale page sale sage 

求从fool到sage变换的最短序列是：
fool -> pool -> poll -> pole -> pale -> sale -> sage

接下来使用图来解决这个问题：
分为两步：
第一步，构建图
第二步，根据图找出最短的路径

构建图：思路很简单，每一个单词就是一个顶点。凡是只相差1个字母的两个单词之间就要建立一条边。
如何确定某两个单词之间是否只相差1个字母？我们可以构建一个字典表X，单词fool挖掉一个字母可以是 _ool f_ol fo_l foo_ 这四个。
那么字典X中就有_ool f_ol fo_l foo_ 这四个下标,每个下标对应的值是一个列表，列表中放着满足这个下标规则的单词。例如 _ool 的列表中放着 fool pool cool 这三个单词。每一个这样的列表就是只差1个字母的单词，他们之间就要建立一条边。

# 词梯问题
def buildWordGraph(wordList):   # 传入一个单词列表
    d = {}      # dict
    g = Graph()

    # 字典d中的每一个元素都是一个set集合，每一个集合内的单词都是只差1个字母的单词
    for word in wordList:
        for i in range(len(word)):
            key = word[:i]+"_"+word[i+1:]
            if key not in d:
                d[key] = set()

            d[key].add(word)

    # 建立两个只差1个字母的单词的边。例如 fool 和 cool 之间会建立两条边，一条fool指向cool的边，一条cool指向fool的边。
    # 由于Graph这个类中的边是单向的，所以要对两个顶点建立两条边才能表示双向。
    for bucket in d:
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)

    return g

if __name__ == "__main__":
    wordList = ["fool","foul","foil","fail","fall","pall","pole","poll","pool","cool","pope","pale","page","sale","sage"]
    wordGraph = buildWordGraph(wordList)

 

构建完图之后，我们就要想办法用这个图找到最优解。
在词梯问题中，找最优解应该要用 广度优先算法 BFS

广度优先算法 BFS 是图算法中最基础最常见的算法。

为了跟踪顶点的加入过程，并避免重复顶点，要为顶点增加3个属性
距离distance：从起始顶点到此顶点路径长度；

前驱顶点predecessor：可反向追溯到起点；

颜色color：标识了此顶点是尚未发现（白色）、
已经发现（灰色）、还是已经完成探索（黑色）

还需要用一个队列Queue来对已发现的顶点进行排列决定下一个要探索的顶点（队首顶点）

思路如下：
从起始顶点s开始，作为刚发现的顶点，标注为灰色，距离为0，前驱为None，加入队列，接下来是个循环迭代过程：

从队首取出一个顶点作为当前顶点；遍历当前顶点的邻接顶点，如果是尚未发现的白色顶点（所有顶点默认为白色，白黑灰分别用w,b,g表示），则将其颜色改为灰色（已发现），距离增加1，前驱顶点为当前顶点，加入到队列中（队列是全局的）

遍历完成后，将当前顶点设置为黑色（已探索
过），循环回到步骤1的队首取当前顶点

PS 通过设置前驱和距离，可以用所有的顶点构建成一棵树，某个顶点所在的层数就是顶点所存储的距离distance。
通过前驱可以找到该顶点的父节点。
树里面没有重复顶点。一个顶点就是一个树节点。

例如，要求从 fool变成sage 的最短路径
1.开始顶点是 fool 这个顶点对象，将这个顶点的颜色从白色改为灰色，距离设置为0

2.遍历 fool这个顶点中的相邻点，并且将这些相邻点添加到队列中，并且这些相邻点的distance为fool的distance+1，设置这些相邻点的前驱是fool顶点。

3.遍历完这些相邻点之后，将fool这个顶点的颜色调成黑色。

然后从队列中弹出一个顶点A（队列是先进先出哦），对其重复上述步骤，但是要注意，遍历A的相邻点的时候，如果A的某个相邻点的颜色不是白色的就不用设置距离和前驱，也不用加入队列。否则构建的树中会有重复的节点。

以上寻找fool到sage的过程就是构建一个从fool到sage的树的过程，起点fool是树的根节点，终点sage可能是叶节点也可能是中间节点，其他单词是中间节点和其他叶节点。

他不是真的构建出一棵树对象，而是通过增加和修改图的顶点的一些属性（如 distance 和 prefix前驱）,使得顶点具备了树节点的特性，从而让树节点有了树的逻辑。

将起点到终点的树构建好了以后，我们通过回溯的方式打印出最短路径。
思路是这样的：直接获取sage顶点，根据sage顶点的前驱找到上一个词，这样一直往上找。这个过程是在树上从某个节点一直往上层去查找直到找到根节点fool

下面贴出所有的代码

# 词梯问题

# 为了适应词梯问题，需要对Vertex类进行扩展
class wordVertex(Vertex):
    def __init__(self,key):
        super(wordVertex,self).__init__(key)
        self.distance = 0   # 单词所在树的层数默认为0
        self.color = "w"    # 单词顶点的颜色默认是白色
        self.prefix = None  # 单词顶点的前驱顶点默认是None


# 构建一个单词关系图
def buildWordGraph(wordList):   # 传入一个单词列表
    d = {}      # dict
    g = Graph(wordVertex)

    # 字典d中的每一个元素都是一个set集合，每一个集合内的单词都是只差1个字母的单词
    for word in wordList:
        for i in range(len(word)):
            key = word[:i]+"_"+word[i+1:]
            if key not in d:
                d[key] = set()

            d[key].add(word)

    # 建立两个只差1个字母的单词的边。例如 fool 和 cool 之间会建立两条边，一条fool指向cool的边，一条cool指向fool的边。
    # 由于Graph这个类中的边是单向的，所以要对两个顶点建立两条边才能表示双向。
    for bucket in d:
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)

    return g

# 使用bfs算法构建树
def bfs(start):   # g是单词图，start是开始的单词的顶点对象
    vertQueue = []      # 探索队列
    vertQueue.insert(0,start)

    while len(vertQueue) > 0:
        currentVert = vertQueue.pop()  # 当前探索的顶点
        for nbr in currentVert.getConnections():
            if nbr.color == "w":   # 如果该相邻节点没有探索过才将他放入探索队列中
                nbr.distance = currentVert.distance + 1    # 设置该相邻节点在树中的层数
                nbr.prefix = currentVert    # 设置该相邻节点在树中的父节点
                currentVert.color = "g"  # 设置为正在探索的状态
                vertQueue.insert(0,nbr)    # 进入探索队列
            currentVert.color = "b"     # 设置为已探索状态

# 通过回溯的方式打印出最短路径
def getPath(destination):     # destination是结束的单词的顶点对象
    # 从树的叶节点往上层找,直到找到根节点
    print(destination.key)
    while destination.prefix != None:
        print(destination.prefix.key)
        destination = destination.prefix

if __name__ == "__main__":
    wordList = ["fool","foul","foil","fail","fall","pall","pole","poll","pool","cool","pope","pale","page","sale","sage"]
    wordGraph = buildWordGraph(wordList)
    # print(wordGraph)
    bfs(wordGraph.getVertex("fool"))
    getPath(wordGraph.getVertex("sage"))
    

这里要注意，如果想找 fool 到sage的路径，用广度优先和深度优先算法都可以。但是要找“最短”路径就只能用广度优先。
所以 解决“最短”问题就可以使用广度优先的方法。

简单概括一下词梯问题的解决步骤：
1.构建词梯图
2.构建逻辑的树
3.回溯

 

 

2.骑士周游问题

在一个国际象棋棋盘上，一个棋子“马”（骑士），按照“马走日”的规则，从一个格子出发，要走遍所有棋盘格恰好一次。
把一个这样的走棋序列称为一次“周游”

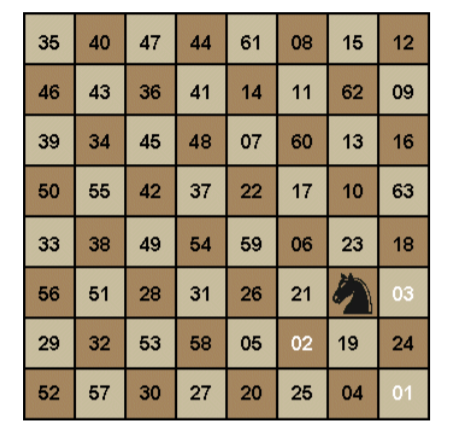
采用图搜索算法，是解决骑士周游问题最容易理解和编程的方案之一

思路：
假设有一个n*n的棋盘，例如8*8，每一个格子都有一个序号，以左下方的格子为第一个格子，序号为0，所以所有格子的序号是0~63
将棋盘构建为图，每一个格子是一个顶点
将所有棋子路径相邻的两个格子作为图的相邻点建立边。例如 

54    55    56    57    58    59    60    61    62
45    46    47    48    49    50    51    52    53
36    37    38    39    40    41    42    43    44
27    28    29    30    31    32    33    34    35
18    19    20    21    22    23    24    25    26
9     10    11    12    13    14    15    16    17
0     1     2     3     4     5     6     7     8

按照马走日，0号格子的相邻格子是11和19。而31号格子的相邻格子是42,40,48,38,20,12,14,24（相邻的格子最多8个）

这样子建立好了图之后，我想获取一次周游的路径该怎么做？

可以使用深度优先算法。
具体做法是：从某一个格子出发，按照图中顶点的边一直走，但是途中不能走重复的格子。使用一个计数器，如果计数器到达63则表示成功周游了一次棋盘的所有格子。
如果走到某一个格子X，它有k个相邻的格子，走第1个发现之前走过，那么退回去再走第二个，如果一直都到第k个，发现第k个还是走过，那么就要退回格子X的上一个格子，再重复这个过程。
所以这里需要一个栈来记录走过的格子，通过栈后进先出的特性方便回退。
由于这是一个重复的过程，所以可以使用递归调用。

代码如下：# 骑士周游问题

# 构建棋盘图
def buildChaseGraph(bsize=5):     # bsize是棋盘大小，默认是5
    g = Graph(wordVertex)   # 由于棋盘问题的每个格子需要设置颜色以标明状态，所以这里使用wordVertex这个节点
    ways = [(-1,-2),(-2,-1),(1,-2),(2,-1),(2,1),(1,2),(-1,2),(-2,1)]     # 方位有8个

    for y in range(bsize):
        for x in range(bsize):    # 一个格子一个格子的遍历
            id = getPos(x,y,bsize)  # 获取当前格子的序号
            for way in ways:
                if not outOfChase(x+way[0],y+way[1],bsize):  #  判断相邻格子是否超出边界，只留下没有超出边界的格子可以作为当前格子的相邻顶点
                    nbrId = getPos(x+way[0],y+way[1],bsize)   # 获取相邻格子的序号
                    g.addEdge(id,nbrId)

    return g

# 根据横纵坐标获取格子的序号,例如5*5的棋盘中，x=1,y=2的格子序号是11
# 其中第一个格子（左下角的格子）其坐标是 (0,0)
def getPos(x,y,bsize):
    return x+y*bsize

# 判断坐标是否超过棋盘范围
def outOfChase(x,y,bsize):
    if x < 0 or x>=bsize or y<0 or y>=bsize:
        return True
    else:
        return False

# 获取一个周游路径
def getPath(current,bsize,stack=[]):   # g是建立好的图，current是开始的格子的顶点,stack是用于记录路径的栈（用列表模拟栈）
    stack.append(current.key)
    current.color = "g"   # 标记该格子已探索

    if len(stack) == bsize*bsize:
        done = True
    else:
        done = False
        nbrs = list(current.getConnections())
        # print(nbrs)
        i=0
        while i < len(nbrs) and not done:
            if nbrs[i].color == "w":
                done = getPath(nbrs[i],bsize,stack)
            i += 1

        if not done:
            current.color = "w"
            stack.pop()

    return done

if __name__ == "__main__":
    cg = buildChaseGraph(6)
    print(cg)
    stack = []
    print(getPath(cg.getVertex(6),6,stack))
    print(stack)

    
上面的getPath，其实可以用 if nbrs[i].key not in stack 判断nbrs[i]是否被探索过，但是 列表的 in 操作是O(n)，所以用 color 属性标记是否已探索过。典型的空间换时间。

上述算法的性能高度依赖于棋盘大小：
就5×5棋盘，约1.5秒可以得到一个周游路径
但8×8棋盘，则要半个小时以上才能得到一个解

目前实现的算法，其复杂度为O(kn)，其中n是棋盘格数目
这是一个指数时间复杂度的算法！其搜索过程表现为一个层次为n的树

=====================================================================
我们可以做一个小小的改进，当我走到了节点A的时候，我要往节点A的相邻节点走。假如A有5个相邻节点，这5个相邻节点里面有4个是没有探索过的。
这个时候我们可以挑这4个顶点里面，其相邻顶点（没有探索过的）数最少的先探索。
例如 A 的这4个相邻顶点是 B C D E 
B 的未探索过的相邻顶点有 B1 B2 B3 B4 B5 这5个
C 的未探索过的相邻顶点有 C1 C2 C3 这3个
D 的未探索过的相邻顶点有 D1 D2 D3 D4 这4个
E 的未探索过的相邻顶点有 E1 E2 这2个

那么就对B~E 这4个顶点排序，按照 E C D B 的顺序探索。挑相邻顶点最少的顶点探索。

# 对顶点 vert 的相邻顶点排序
def orderByAvail(vert):
    orderList = []
    for nbr1 in vert.getConnections():
        if nbr1.color == "w":
            c = 0   # 记录vert的每个相邻顶点的相邻顶点的个数
            for nbr2 in nbr1.getConnections():
                if nbr2.color == "w":
                    c += 1
            orderList.append((c,nbr1))

    # 对vert的相邻顶点排序
    orderList.sort(key=lambda x:x[0])

    return [y[1] for y in orderList]

然后对 getPath 进行修改：

def getPath(current,bsize,stack=[]):   
    stack.append(current.key)
    current.color = "g"

    if len(stack) == bsize*bsize:
        done = True
    else:
        done = False
        # nbrs = list(current.getConnections())   # 未改进的做法（不对current的相邻点排序）
        nbrs = orderByAvail(current)                # 改进的做法（对current的相邻点排序）

        i=0
        while i < len(nbrs) and not done:
            if nbrs[i].color == "w":
                done = getPath(nbrs[i],bsize,stack)
            i += 1

        if not done:
            current.color = "w"
            stack.pop()

    return done
    

 

 

深度优先算法

骑士周游问题是一种特殊的对图进行深度优先搜索
其目的是建立一个没有分支的最深的深度优先树
表现为一条线性的包含所有节点的退化树

接下来实现一个通用的深度优先算法。
这个算法是这样的，遍历所有的顶点，并且对遍历的顶点沿着它的有向边进行探索直到所有顶点被探索完。

结果是：会构建出一棵树或者多棵树（森林）

什么情况会构建出一棵树，什么时候会构建出森林？
例如 

 

如果从A出发进行探索，就会构建出一棵树，如下

         A
         |     
         B  
         |
        ---
       |   |
       C   D
           |
           E 
           |
           F

           
如果是从E出发探索（往EB方向先探索） 可以构建出两棵树

         E               A
         |               |
        ---              D
       |   |   和 
       B   F 
       |
       C

（由于E经过多个顶点不能指向A，所以将E的所有能连接的顶点连完之后就又要从A顶点开始探索）

就算是从同一个顶点，往不同方向也会有不同的森林。
例如从E出发探索（往EF方向先探索） 还可以构建出

         E               A
         |               
        ---              
       |   |   和 
       B   F 
       |   |
       D   C

图中有多少个顶点，树就有多少个节点。

此外，还要设置“发现时间”和“结束时间”属性
前者是在第几步访问到这个顶点（设置灰色）
后者是在第几步完成了此顶点探索（设置黑色）

# 带有深度优先算法的图
class DFSVertex(Vertex):    # 为dfs算法而设的顶点
    def __init__(self,key):
        super(DFSVertex,self).__init__(key)
        self.st = 0   # 顶点开始被探索的时间点
        self.et = 0   # 顶点被探索完成的时间点
        self.color = "w"    # 节点状态，g是正在被探索，b是已被探索
        self.prefix = None  # 节点的前置节点，该属性可以让我们知道该节点在其所在的树中的父节点是谁

class DFSGraph(Graph):
    def __init__(self):
        super(DFSGraph, self).__init__()
        self.time = 0

    # 深度优先算法对图构建树或者森林
    def dfs(self):
        for aVertex in self.vertList:    # 将所有顶点的状态设为初始状态（未探索过，前置为空）
            aVertex.color = "w"
            aVertex.prefix = None

        # 开始探索所有的顶点
        for aVertex in self.vertList.values():
            if aVertex.color == "w":  # 只探索未探索过的节点
                self.explore(aVertex)

    # 探索节点（就是不停的往节点的下层找相邻节点）
    def explore(self,aVertex):      # 从dfs()内部调用explore()传进来的aVertex全都是起始顶点（也是树的根节点）
        aVertex.color = "g"     # 标记为正在探索
        self.time += 1
        aVertex.st = self.time  # 标记开始探索时间

        # 对该节点的相邻节点进行探索
        for nbr in aVertex.getConnections():
            if nbr.color == "w":
                nbr.prefix = aVertex    # 标记前置节点
                self.explore(nbr.color)

        # 探索完该节点和该节点的所有下层节点后
        aVertex.color = "b"     # 标记该节点为已探索
        self.time += 1
        aVertex.et = self.time  # 标记探索完的时间

 

       
最短路径算法
以互联网的网路为例，数据包从起始主机A发出到达目标主机B需要经过很多路由器和网关。从A到B可以经过的路由器和网关的组合有很多，但是为了保证网络传输的时间最短，我们希望经过的路由器也越少。
互联网就是一个图，路由器和网关就是一个个中间节点，最短路径问题可以通过图的算法解决。

其实这个问题在词梯问题中遇到过，将一个单词变成另一个单词，每次只变动一个字母，如何做到变动次数最少。

在这里则有所不同，假设每个路由器之间的距离是不同的，例如有 C1~5 这5个路由器，A到B有以下几条路径
     2
   |--->C1
   | 4   |1 1
A -|--->C3--->B<--|
   |  1     3     |2
   |---->C2---C4--|
   
上图的数字是节点之间的距离
有 
A-C1-C3-B       总距离4
A-C3-B          总距离5
A-C2-C4-B       总距离7
三条路径 但是明显第一个方案最短

所以这里的最短问题和词梯问题不同在于节点和节点之间是有距离而且距离不等。词梯问题则是节点和节点的距离全都为1

距离体现为节点之间边的权重
这个算法的发明者是Dijkstra，所以叫做Dijkstra算法

理论思路如下：
假设一个图有10个顶点A1~10, 我想得到A1到A5的最短路径。
Dijkstra算法不是直接去算 A1到A5的最短路径，而是将A1到A2~10 这9个点的最短路径全都算出来然后存起来。

这样我不仅可以找到 A1到A5的最短路径，还可以找到A1到A2~10的任何一个节点的最短路径。

这里不得不画图说明：

如图所示
以u点为出发点：先遍历u的所有邻接点，计算距离，
u和v,w,x 的直接距离为2,5,1 
但是u还可以通过v到达w,v到w距离是3，u-v-w距离是5，等于u-w（u直接到w）的距离

u还可以通过x到达w,x到w距离是3，u-x-w距离是4，小于u-w（u直接到w）的距离5

所以u到达w的真实距离为5

以此类推

程序上该怎样实现上述理论思路？
顶点的访问次序由一个优先队列来控制，队列中作为优先级的是顶点的dist属性（即distance，即该顶点到开始点的真实距离）。
相邻顶点间的距离是边的权重weight。
当且仅当某顶点X是开始点Y的相邻点，而且X到Y的直接距离小于X途径其他顶点到Y的距离时 dist属性才等于weight。

最初，只有开始顶点dist设为0，而其他所有顶点dist设为sys.maxsize（最大整数），全部加入优先队列。（dist越小，顶点优先级最高）
随着队列中每个最低dist顶点率先出队并计算它与邻接顶点的权重，会引起其它顶点dist（该顶点到开始点的真实距离）的减小和修改，引起堆重排
并据更新后的dist优先级再依次出队

Dijkstra算法只能处理大于0的权重
如果图中出现负数权重，则算法会陷入无限循环

Dijkstra算法需要具备整个图的数据，而且节点不能变动（不能添加或者删减顶点，或者移动顶点位置），否则计算出来的最短路径会失效

# 最短路径算法
class shortVert(Vertex):
    def __init__(self,key,dist=0):
        super(shortVert,self).__init__(key)
        self.dist = dist   # 记录该节点和某一个节点间的距离
        self.pred = None    # 记录该节点的前驱（该前驱只针对以某一个作为起点的最短路径的前驱，也就是说，换一个起点这个前驱就会变）

# 这里我们使用一个有序队列实现优先队列
class PriorityQueue:
    def __init__(self,queue=[]):
        self.queue = queue     # 列表中的元素顶点对象
        self.buildQueue()

    # 添加一个元素，自动给改元素排序
    def push(self,item):
        self.queue.append(item)
        self.sortLastItem()

    # 弹出最小元素
    def pop(self):
        return self.queue.pop()

    def sortLastItem(self):
        itemPos = len(self.queue) - 1  # i是新添加的元素的位置
        finished = False
        while itemPos > 0 and not finished:
            if self.queue[itemPos].dist > self.queue[itemPos - 1].dist:
                self.queue[itemPos], self.queue[itemPos - 1] = self.queue[itemPos - 1], self.queue[itemPos]
                itemPos -= 1  # 更新新添加元素的位置
            else:
                finished = True

    # 给一个元素重新排序，del的复杂度是O(n)，所以不推荐使用
    # def resetPos(self,item):
    #     itemPos = 0
    #
    #     while itemPos < len(self.queue):
    #         if self.queue[itemPos] == item:
    #             break
    #         else:
    #             itemPos += 1
    #
    #     itemReset = self.queue[itemPos]
    #     del(self.queue[itemPos])
    #     self.push(itemReset)

    def resetPos(self,item,val):
        itemPos = 0

        # 根据元素值查找下标，其实可以用 self.queue.index(item)代替
        while itemPos < len(self.queue):
            if self.queue[itemPos] == item:
                break
            else:
                itemPos += 1

        # 修改节点的dist值
        item.dist = val

        finished = False
        while itemPos < len(self.queue)-1 and not finished:
            if self.queue[itemPos].dist < self.queue[itemPos+1].dist:
                self.queue[itemPos],self.queue[itemPos+1] = self.queue[itemPos+1],self.queue[itemPos]
                itemPos += 1
            else:
                finished = True
        
        finished = False
        while itemPos > 0 and not finished:
            if self.queue[itemPos].dist > self.queue[itemPos-1].dist:
                self.queue[itemPos],self.queue[itemPos-1] = self.queue[itemPos-1],self.queue[itemPos]
                itemPos -= 1
            else:
                finished = True

    # 构建一个优先队列(其实就是排序)
    def buildQueue(self):
        self.queue = self.__class__.quickSort(self.queue)

    # 使用快排法排序(这里排出来的是个倒序的)
    @classmethod
    def quickSort(cls,aList):
        if len(aList) <= 1:
            return aList
        # print(aList)
        mid = aList[0]
        left = []
        right = []

        for index in range(1,len(aList)):
            if aList[index].dist < mid.dist:
                right.append(aList[index])
            else:
                left.append(aList[index])
                
        left = cls.quickSort(left)
        right = cls.quickSort(right)

        return left + [mid] + right

    def __str__(self):
        return str([{vert.key:vert.dist} for vert in self.queue])

# 设置图中针对某一节点为起点的最短路径
import sys
def setShort(g,start):  # g是图，start是起点顶点
    # dist距离指某节点相对起点的真实距离。
    # 初始将图中起点的dist设为0，其他所有节点的dist设置为sys.maxsize
    # 将所有节点放入优先队列
    pq = PriorityQueue()
    for vert in g.vertList.values():
        vert.pred = None
        if start == vert:
            vert.dist = 0
        else:
            vert.dist = sys.maxsize

        pq.push(vert)

    # 当优先队列的元素为空则起点到其他所有顶点的最短路径就已经设置好了
    # 下面这段代码的作用是对所有非start的节点设置前驱
    # 之后查找start到顶点A的最短距离则是通过回溯A的前驱来完成的
    while len(pq.queue) > 0:
        nowVert = pq.pop()  # 弹出距离最短的节点；第一个弹出的节点肯定是start；优先队列中元素位置会随着距离的更新而改变

        # 设置当前节点的相邻节点的dist
        for nbr in nowVert.getConnections():
            newDist = nowVert.dist + nowVert.getWeight(nbr)     #  nbr的新距离等于nowVert到起点的距离+nbr到nowVert的距离

            # 如果nbr的新距离比nbr的旧距离短则更新nbr的距离
            if newDist < nbr.dist:
                pq.resetPos(nbr,newDist)   # 更新nbr的距离，同时改变nbr在优先队列中的位置
                nbr.pred = nowVert          # 设置nbr的前驱

# 获取最短路径
def getShort(start,destination):      # 传入起点和终点2个顶点
    path = []
    curVert = destination
    while curVert.pred:
        path.append(curVert.key)
        curVert = curVert.pred

    path.append(start.key)
    path.reverse()

    return path

if __name__ == "__main__":
    # 构建一个有距离的图
    g = Graph(shortVert)
    g.addEdge("u","v",2,True)
    g.addEdge("u","w",5,True)
    g.addEdge("u","x",1,True)
    g.addEdge("v","w",3,True)
    g.addEdge("v","x",2,True)
    g.addEdge("x","w",3,True)
    g.addEdge("x","y",1,True)
    g.addEdge("w","y",1,True)
    g.addEdge("w","z",5,True)
    g.addEdge("y","z",1,True)

    start = g.getVertex("u")
    end = g.getVertex("z")
    setShort(g,start)
    path = getShort(start,end)
    print(path)

最关键的代码是setshort()

=================================================

最小生成树

最小生成树可以用来解决广播问题。
例如说，系统有一个消息要广播给所有局域网内的用户（局域网内路由器有7个分别是A~G，共有四个用户分别在C，D，E，G），那么这个消息从出发点A怎么到达这4个用户。

方法1：
A分别发送四次相同的消息，每次的消息会按照最短路径到达C,D,E,G 
此时持有消息的路由器为 A,C,D,E,G 和中间途径过的路由器
这种方法叫做单播解法

方法2：
每个节点发k次消息，k是该节点的所有相邻点的个数。例如A的相邻点有BC，则A会发两次消息，第一次发给B，第二次发给C
而B的相邻点有DEC，B就会发三次消息，分别给DEC
...
此时持有消息的路由器为图中所有的路由器
这种方法叫做洪水解法（暴力解法）

信息广播问题的暴力解法，是将每条消息在路由器间散布出去
所有的路由器都将收到的消息转发到自己相邻的路由器和收听者
显然，如果没有任何限制，这个方法将造成网络洪水灾难
很多路由器和收听者会不断重复收到相同的消息，永不停止！

所以，洪水解法一般会给每条消息附加一个生命值（TTL:TimeToLive），初始设置为从消息源到最远的收听者的距离；
每个路由器收到一条消息，如果其TTL值大于0，则将TTL减少1，再转发出去
如果TTL等于0了，则就直接抛弃这个消息。
TTL的设置防止了灾难发生，但这种洪水解法显然比前述的单播方法所产生的流量还要大。

信息广播问题的最优解法，依赖于路由器关系图上选取具有最小权重的生成树（minimumweightspanningtree）
生成树：拥有图中所有的顶点和最少数量和权重的边，以保持连通的子图。

图G(V,E)的最小生成树T，定义为
包含所有顶点V，以及E的无圈子集，并且边权重之和最小

解决最小生成树问题的Prim算法，属于“贪心算法”，即每步都沿着最小权重的边向前搜索。
构造最小生成树的思路很简单，如果T还不是生成树，则反复做：
找到一条最小权重的可以安全添加的边，将边添加到树T
“可以安全添加”的边，定义为一端顶点在树中，另一端不在树中的边，以便保持树的无圈特性

例如下面的图片有一个图(图中的边的权重可以看成是数据包传输所花费的代价，为了减小这个代价，我们希望广播的时候，信息发送的总次数最少，而且经过的边的权重之和最小)：
他的最小生成树是黄色箭头指向的分支。
也就是这样的一棵树：

            A
            |     
            B
            |
         ------
        |      |
        D*     C*
        |
        E*
        |
        F
        |
        G*
        
现在我们要生成这个树# 最小生成树

# 该算法的实现和最短距离几乎一模一样，但是最小生成树算法中的dist不是某节点X到起点的距离，而是X的上游相邻节点们到X的距离的最小的那个距离
def prim(g,start):
    pq = PriorityQueue()
    for vert in g.vertList.values():
        vert.pred = None
        if vert == start:
            vert.dist = 0
        else:
            vert.dist = sys.maxsize
    

    while len(pq.queue) > 0:
        nowVert = pq.pop()      

        for nbr in nowVert.getConnections():
            newDist = nowVert.getWeight(nbr)    # *diff
            if nbr in pq.queue and newDist < nbr.dist:  # *diff
                pq.resetPos(nbr,newDist)   # 更新nbr的距离，同时改变nbr在优先队列中的位置
                nbr.pred = nowVert

该算法的实现和最短距离几乎一模一样，但是最小生成树算法中的dist不是某节点X到起点的距离，而是X的上游相邻节点们到X的距离的最小的那个距离

什么叫做上游节点，例如上面图片中ABF是C的相邻节点，但A和B是C的上游相邻节点，F不是。原因是，当从优先队列中取出F的时候，C早已经从优先队列被弹出！

标记了# *diff的地方就是和最短距离算法不同的地方

===================================================

PS：最小生成树和最短路径的图中的边都是无向边！