本文内容参考《redis设计与实现》一书总结归纳而得。

整数集合

整数集合本质是一个整数数组，它是set集合类型的底层实现之一。当一个集合只包含少量整数元素时redis会用整数集合作为集合的底层数据结构。

我们看看整数集合对象的构成：

typedef struct intset { 
// 编码方式 
uint32_t encoding; 

// 集合包含的元素数量 
uint32_t length; 

// 保存元素的数组 
int8_t contents[]; 
} intset; 

encoding

inset可以保存 int16_t/int32_t/int64_t这3种整型，encoding属性记录整数集合保存的整数元素是哪种整型。

contents

contents数组保存的整型类型取决于 intset的encoding属性而非int8_t。而且contents中的元素是从小到大排好序，并且不含重复值的。

length

length属性记录了contents数组的长度。

intset结构如下图所示：

升级和降级

当某个新元素要添加到intset中并且该新元素的类型长度比其他元素大（比如原数组中存放的是int16类型的整型，后来新增的元素是int32类型的整型）就会引发contents数组升级，升级会为contents重新分配内存空间，然后新元素才会被加到intset中。

升级过程如下：

1. 根据新元素的int类型，为已有intset的contents重新分配空间（在原有contents数组上扩展，而非创建一个新contents数组），分配的空间能够放下转换类型后的已有元素和新元素。

2. 将原来contents的所有元素转为新元素的类型，并将这些元素放到扩展后contents的正确位置，要保持有序性不变。

3. 将新元素添加到新的contents中。

举例说明：

原intset的contents为int16类型的数组：

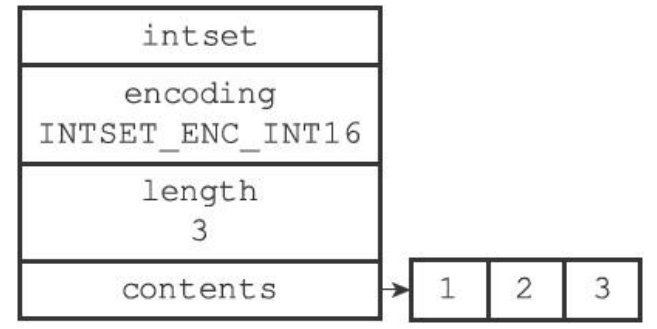
里面的每个元素只占16位：

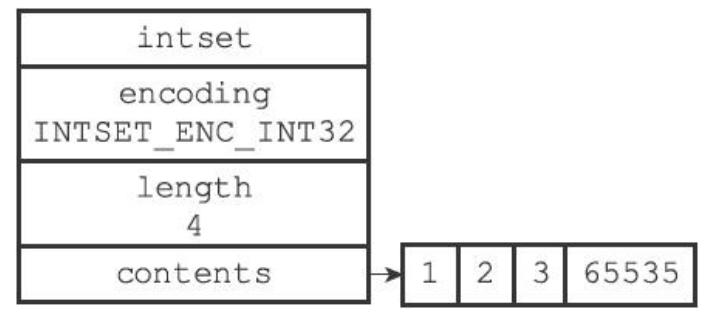
现在我要插入一个整数为int32的 65535，已知int16的范围在-32768~32767之间，所以65535肯定是超过int16的长度范围的，因此65535只能是int32或int64类型。

此时会引发为原有contents数组扩展，redis会计算需要扩展多少空间：一共有4个元素，每个元素的长度都是32位，4*32=128，128-3*16 = 128-48=80。所以这个数组要扩展80个位变成：

再把1，2，3转为32位整数，并放到对应的位上（注意它是按321的顺序放而不是123，因为它新分配的空间在数组尾部，如果按321放只需在原数组上移位即可，如果按123的顺序放，为了不让32位的1把数组元素2给覆盖掉，需要创建一个额外的数组来放置，浪费空间）：

最终变成

最后修改intset的encoding和length属性：

插入一个新元素如果不引发升级，由于数组是有序的，因此插入的复杂度为O(log n)，插入引起的其他元素的顺位后移所以复杂度会为O(n)。

如果会引发升级，会引起所有的元素转换类型并重新放置到合适的位，因此复杂度为O(n)，新插入的元素要么大于所有元素，要么小于所有元素，所以这个元素会被放在开头或者末尾。

如果int64的contents数组中插入int32，那么redis会将其先转为int64再插入。

升级的优点：一个是灵活性，通过升级允许数组可以插入不同类型的int（通过升级底层数组来适应新元素），不像C语言那样对于一个int16的数组就不能再插入int32的整型；一个是节约内存，一个能同时存储int16/int32/in64的数组最简单的做法就是直接用int64的数组来存储，但这意味着即使集合存储的是int16/int32也要将其转为int64再存，从而浪费内存。升级操作使得数组只有在需要的时候再申请更多空间去存，节省了内存。

整数集合不支持降级，一旦数组升级从int16变成int32或int64，或者从int32变成int64后，该数组的编码会一直保持在升级后的状态（也就是不会降级为int32或int16）。因为要做到降级，redis必须在每删除一个整数元素后检查一遍剩余所有元素是否符合降级的类型要求，这无疑会大大的降低删除操作的效率。

综上，整数集合的插入和删除复杂度为O(n)，因为插入和删除会引发其他元素的批量位移；而查询的复杂度为O(logN)，因为数组是有序的，可以通过二分查找来查询；随机获取一个元素的复杂度为O(1)，因为在知道数组占的空间位数和数组的开始地址以及每个元素所占位数，只需将指针定位到数组的某个元素的位即可。

更多内容请关注微信公众号