本文内容参考《redis设计与实现》一书总结归纳而得。

压缩链表

压缩列表本质是一系列特殊编码（方式）的连续内存块组成的顺序型数据结构。该结构从左到右包含zlbytes（压缩列表占用字节数）、zltail（压缩列表最后一个节点开始地址，是个相对地址）、zllen(压缩列表节点数)、entryX（压缩列表包含的节点，可以有多个节点）、zlend（一个单字节，用于标记到达了压缩列表的末端）。这些属性在一个压缩列表的内存空间中是紧密相连的。

如图所示：

PS：该图的每一个小内存块存的都是实际值而非指针，比如entry1~entryN，图中的每个小块存的不是entry节点的指针，而是entry节点的实际内容。而且entry不会保存redisObj对象，在其他结构中，如果要在复杂数据结构中保存一个字符串，那么其实是保存一个字符串的redisObj对象，但是在压缩列表entry中，保存的是一个entry对象封装的字符串。

压缩列表节点entryX

一个压缩列表节点包含3个属性：previous_entry_length(上一个节点的长度)，encoding(编码类型，分为整型和字符串数组)和content(节点内容)

previous_entry_length

记录前一个entry节点的长度，用当前entry节点的起始地址的指针c减去当前entry节点的previous_entry_length属性可以得到上一个节点的起始地址指针p。通过这个方法可以快速完成表尾节点到表头节点的遍历。

previous_entry_length的长度为1字节（前一个节点长度小于254字节的情况下）或5字节（前一个节点长度大于254字节的情况下，此时previous_entry_length的第一个字节会被置为0xFE，后四个字节保存前一个节点的长度）。

encoding

编码方式，记录该节点该如何编码和解编码（即记录节点的类型和长度）。

encoding的长度为一字节或两字节或五字节。

encoding的最高2位为00、01或10的表示是字节数组，最高2位为11表示是整型，字节数组和整型的长度为encoding去掉最高两位的其他位记录。

字节数组编码

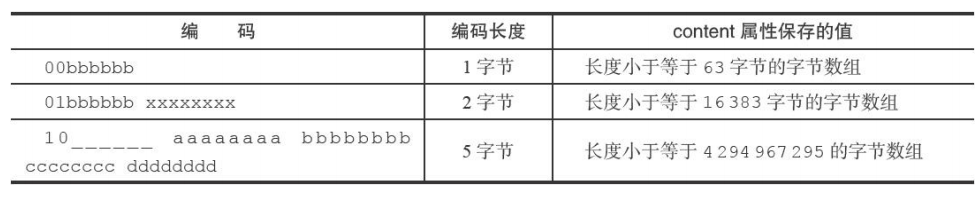
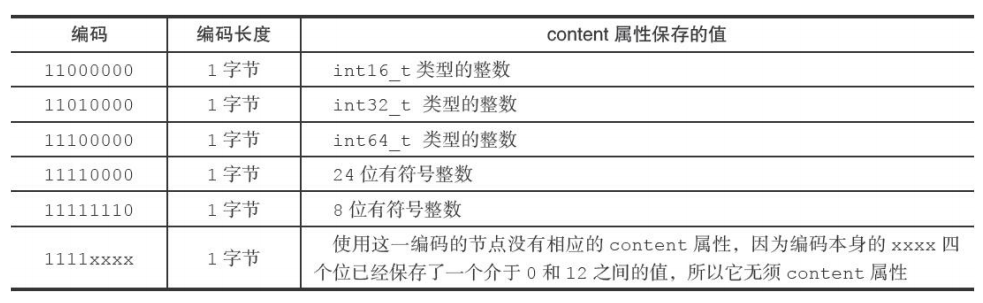
content

保存一个字节数组（字节数组是每个下标放一个字符）或者一个整型，值的类型和长度有encoding决定。

如下如为一个entry节点

entry1~entryN可以全为字符串数组节点，或者全为整型节点，也可以是字符串数组节点和整型节点混合，也可以是不同长度的整型节点的混合。

连锁更新

考虑一种情况，当修改一个节点（使其长度增加）或者往头部插入一个节点，假设这个节点长度为n个字节，那么这个节点后面的所有节点都要往后挪n个字节的长度，也就是说后面的节点的起始地址都要加n。因此其插入或者删除的复杂度为O(n)。

已知previous_entry_length属性长度为1或5字节。

现在考虑一种极端的情况，修改一个节点（使其长度增加）或者往头部插入一个节点A，假设这个节点长度为n个字节，且n>254，且后面的节点的长度都在251~253之间。

当所有节点完成1次后挪之后，节点A的后一个节点B的previous_entry_length会从1字节变为5字节，所以redis需要系统为节点B重新分配空间（多分配4字节），节点B以后的节点都要再往后挪4字节。

由于节点B长度从251变成255，所以B下一个节点C的previous_entry_length会从1字节变为5字节，于是重复上面的情况。

后面的节点会重复上面的情况，假设一共有N个节点，就一共完成了 N + (N-1) + ... +1 = (N+1)*N/2次节点移动和N次内存空间的分配，此时复杂度为O(N^2)。

这就是所谓的连锁升级。

连锁更新发生的概率很低，而且在节点数量很少的情况下，即使发生连锁更新也不会对性能有影响。

压缩列表的好处是通过将节点紧凑相连可以节约内存，而且在数据量小的情况下访问速度反而更快。

更多内容请关注微信公众号