我们可以简单的把内存看成是一系列连续的以字节为单位的存储空间组成的大存储空间，每一个字节为单位的小存储空间都有一个32位或64位的内存地址。

当需要存储多项数据时，我们可以使用两种基本的数据结构：数组和链表。而实际上我们可以认为所有数据结构一共只有数组和链表这2种，因为所有数据结构如树、图、散列表、队列和栈等都是以数组和链表为基础构建而成的。

 

·数组

数组是在内存中连续存储的有限个相同类型的变量组成的集合。数组中的每个元素在内存中是紧密排列的，而且由于元素的类型相同，因此每个元素的长度相同。

 

下图为数组在内存中的存储形式：

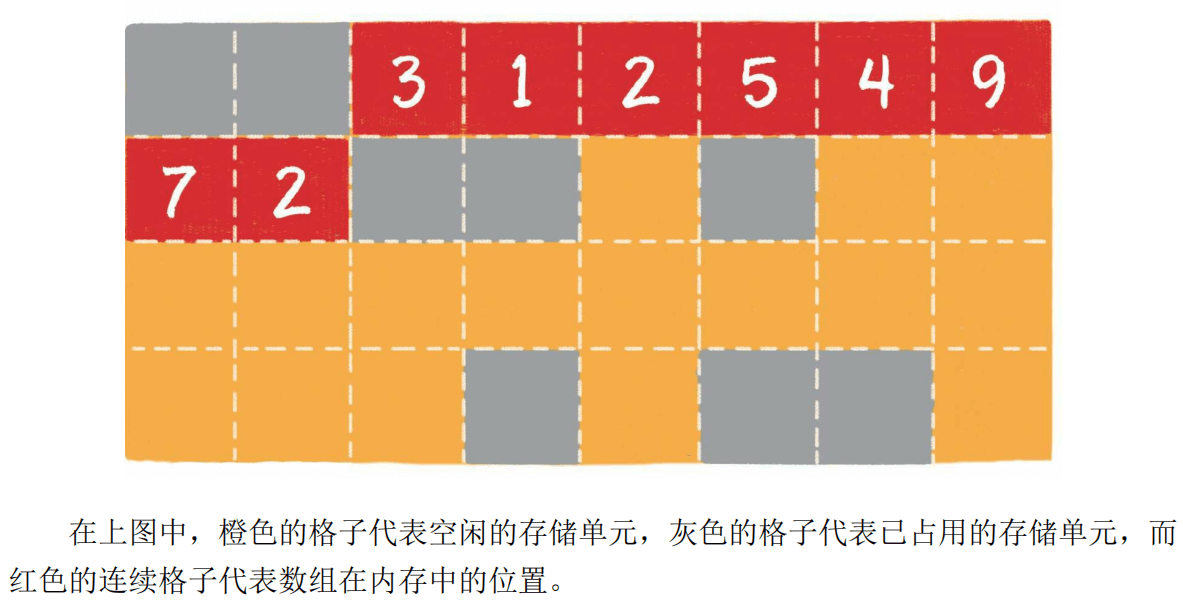
不同类型的数组，每个元素占用的字节数不同，例如对于int16类型的数组，每个元素会占2个字节（即上图中的2个小格子）；对于char类型的数组，每个元素会占1个字节即图中的1个小格子。

创建一个数组需要指定数组元素的个数和类型，计算机会根据类型和元素个数计算这个数组需要占用多少字节的内存空间（即占用多少个小格子），然后向计算机申请一块连续的n个字节的空闲空间存放这个数组。

 

·数组增删改查

查找

每一个数组元素都有一个下标表示该元素的位置，通过某个下标(假设该下标为k)计算机会根据数组的开始地址（即数组第一个元素的开始地址，假设是x）、下标索引(k)和元素的长度(假设是4字节)计算出该元素的开始地址(x+4k)，从而查到该元素的内容。

因此计算机能以O(1)复杂度读取数组的任意一个元素，而无需从数组的第一个元素往后读取到第k个元素。这种读取方式叫做随机读取，随机读取的复杂度为O(1)。

 

更新

更新一个元素其实就是先查找后更改，因此复杂度就是查找的复杂度，为O(1)。

 

插入

插入需要考虑3种情况：

1、尾部插入（插入后元素个数没有超过数组长度），复杂度O(1)

 

2、中间插入（插入后元素个数没有超过数组长度），该操作会导致插入位置之后的元素全部后移一个元素的长度，复杂度为O(n)

 

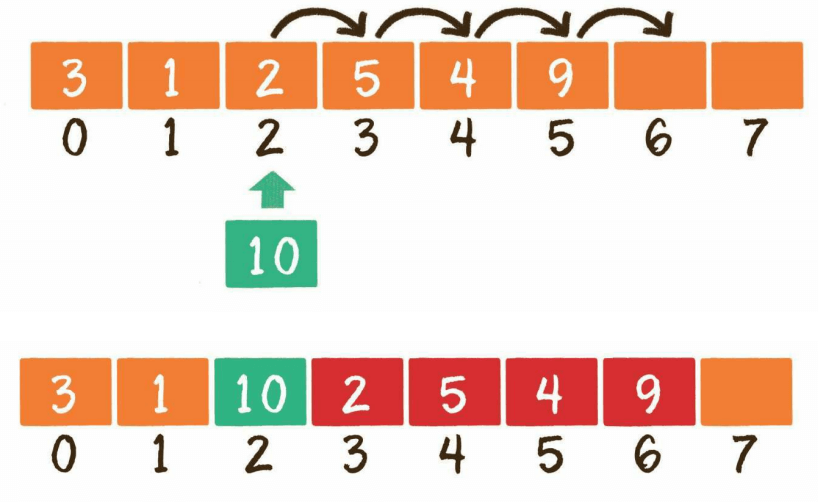
3、超范围插入（插入后元素个数超过数组长度），该情况在插入前需要先判断插入后元素个数是否会超过数组长度，如果超过则需要先对数组扩容，假设扩容默认扩为原数组2倍。扩容操作本质上是在空闲内存中找一块大小为原数组2倍的空间，并拷贝原数组空间的所有元素到新空间，将新数组的指针赋值给变量，最后释放旧数组的空间。该操作涉及所有元素的拷贝，复杂度为O(n)。

 

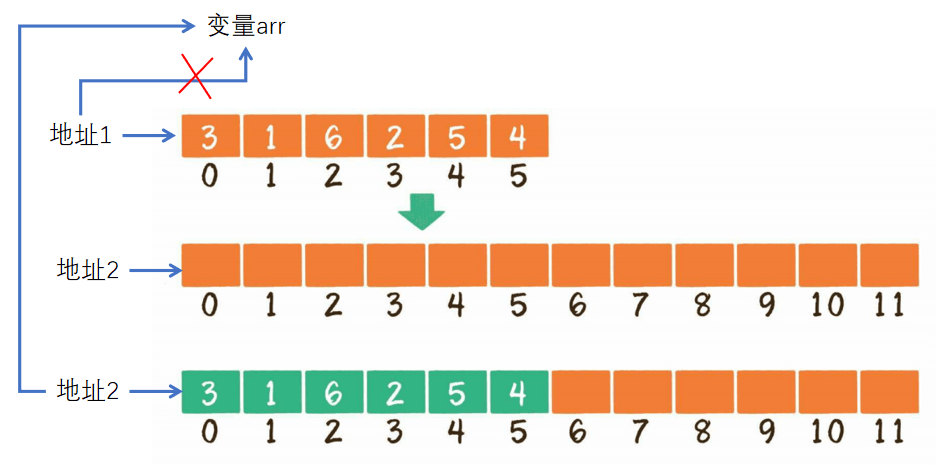
计算复杂度是以最坏复杂度为准，因此插入的复杂度是O(n)。如果不分配额外的空间就会导致内存空间溢出，可能会意外的修改到其他变量内存空间的内容。

 

删除

分两种情况：删除的元素是尾部元素O(1) 和 删除的元素是中间元素O(n)，后者涉及到后面元素的左移。所以删除的复杂度是O(n)。

 

考虑一种取巧的删除方式，假如删除某个元素后不要求保持数组的顺序，我们可以将尾部元素覆盖到要删除的元素，再删除尾部元素，此时复杂度为O(1)。

 

 

·数组优势

随机访问，查询和更改单个元素为常量级时间复杂度。二分查找法就是利用了数组的随机访问特性，每次定位到中间元素的复杂度为O(1)。

 

·数组劣势

插入和删除元素导致后面的元素移动，并可能需要重新分配内存空间导致整个数组的拷贝，效率较低。

 

数组存储字符串

我们知道一些强类型语言中数组元素的类型必须是一致的，每个元素长度是定长的，正因如此，数组才能实现O(1)的随机查找。

那么有没有想过一个数组如何存储多个字符串，我们知道每一个字符串的长度是不同的，此时多个长度不同的字符串该如何被存到数组中？

 

首先我们要知道一个字符串是如何被存储的，这里假设我们存的字符串都是英文。

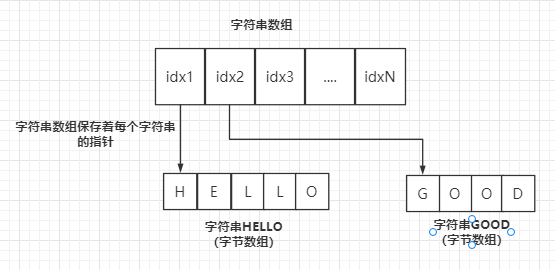
一个字符串由多个字符组成(char类型，占1字节)，字符串就是一个字符类型的数组。 

一个数组保存多个字符串，只需让这个数组的 元素存储这些字符数组的指针即可。指针的长度都是一致的，统一是4字节（32位）或8字节(64位)。

 

 

·链表

链表是一种由多个节点组成的在逻辑上连续，物理上非连续的数据结构。单向链表的节点包括值和指向下一个节点的指针这2部分。

下图是单项链表在内存中的存储形式

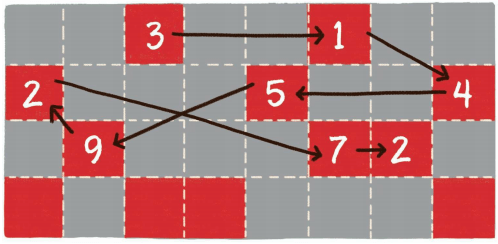
可以看出每个节点元素不是紧密相连的（随机存储），甚至于每个节点的长度可以是不同的，占的内存块不同。

 

由于链表的每个节点是随机的存在内存的各个地方，因此无需分配给链表大块的空闲空间，而是利用起零散的碎片空间。

 

 

·（单向）链表增删改查

一般我们构建一个单向链表结构的时候，需要创建两个结构体：链表节点和链表。在结构体中保存指向第一个节点的指针。

 

 

查询某个节点

需要从头部开始顺着指针往后遍历直到找到指定节点，复杂度O(n)

 

更新某个节点

需要先查询到指定节点再修改节点值，复杂度O(n)

 

 

插入节点有3种情况：

1. 头部插入，只需将新节点的向后指针指向头部节点，并将头部指针指向新节点，复杂度O(1)
2. 中间插入，需要找到指定插入的位置（即先查询），再修改中间节点的指针指向新插入的节点，复杂度O(n)
3. 尾部插入，假如在没有保存尾部节点指针的情况下，需要遍历到尾部节点才能将新节点添加到尾部，复杂度为O(n)。保存了尾部节点指针的情况下复杂度为O(1)。

 

和数组不同的是由于是使用零散空间存储，没有预先定义指定长度，所以无需考虑扩容。

 

删除节点与插入节点相似，也是3种情况，这里不再赘述。

 

需要注意的是，删除某个节点其实就是让其前后节点的指针不再指向该节点，在许多高级语言中我们不用可以释放被删除节点，只要没有指针指向他们，该节点会被自动回收。

 

数组和链表都是线性数据结构，下面是数组和链表的操作时间复杂度（链表更新不考虑先查询的情况下）：

 

 

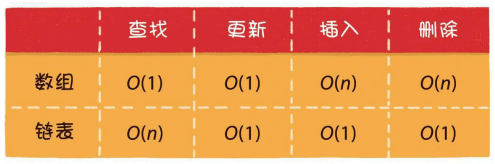
·总体比对

1. 数组需要分配连续的内存空间，且插入元素需要考虑扩容问题；链表节点是非连续存储，无需考虑扩容。
2. 数组查找效率高（随机访问），插入和删除效率较低；链表查找效率低（顺序访问），从头部和尾部插入节点效率高。
3. 链表需要占用额外的内存保存连接节点的指针。

 

一般我们将数组和链表看作是其他数据结构的物理结构。例如树这个逻辑结构，它既可以使用数组构建，也可以用链表构建。