归并排序的思路是将一个长度为n的数组arr，分为arr[:n/2] 和 arr[n/2:]两组，对这两组数组分别再进行归并排序后，将这两组排好序的数组以拉链合并的方式保存在一个额外的长度为n的空数组中。

归并排序使用了递归和分治策略，递归的终止条件是要排序的数组只有1个元素。

 

代码实现如下：

func MergeSort(arr []int) []int{
	var mergeSortHelper func(start, end int)
	mergeSortHelper = func (start, end int){
		if start == end{
			return
		}

		mid := (start + end) / 2		// arr[mid]是左分区的最后一个元素
		mergeSortHelper(start, mid)
		mergeSortHelper(mid+1, end)

		newArr := make([]int, end - start + 1)
		var p, p1, p2 int
		for p, p1, p2 = 0, start, mid+1; p1 <= mid && p2 <= end;p++{
			if arr[p1] > arr[p2]{	// 小的值先进入newArr
				newArr[p] = arr[p2]
				p2++
			}else{
				newArr[p] = arr[p1]
				p1++
			}
		}
		if p1 <= mid{	// 左分组没有全部放入newArr, 需要将左分组剩余元素放入newArr
			for i:=p; i<len(newArr); i++{
				newArr[i] = arr[p1]
				p1++
			}
		}

		if p2 <= end{
			for i:=p; i<len(newArr); i++{
				newArr[i] = arr[p2]
				p2++
			}
		}

		// 将newArr的值覆盖到原数组上
		for i,j:=start,0; i<=end; i, j = i+1, j+1{
			arr[i] = newArr[j]
		}
	}
	mergeSortHelper(0, len(arr)-1)
	return arr
}

从代码可以看出，真正的排序是发生在合并阶段，合并阶段发生在对分组递归排序之后完成，因此归并排序本质是一个二叉树的后续遍历。而快排中，将元素分为比基准元素大和比基准元素小这两个分组的过程是发生在递归之前，因此快排本质上是一个二叉树的前序遍历。

 

复杂度分析

可以画一个二叉树来分析代码中递归函数的调用过程，二叉树的一个节点就是一次递归。

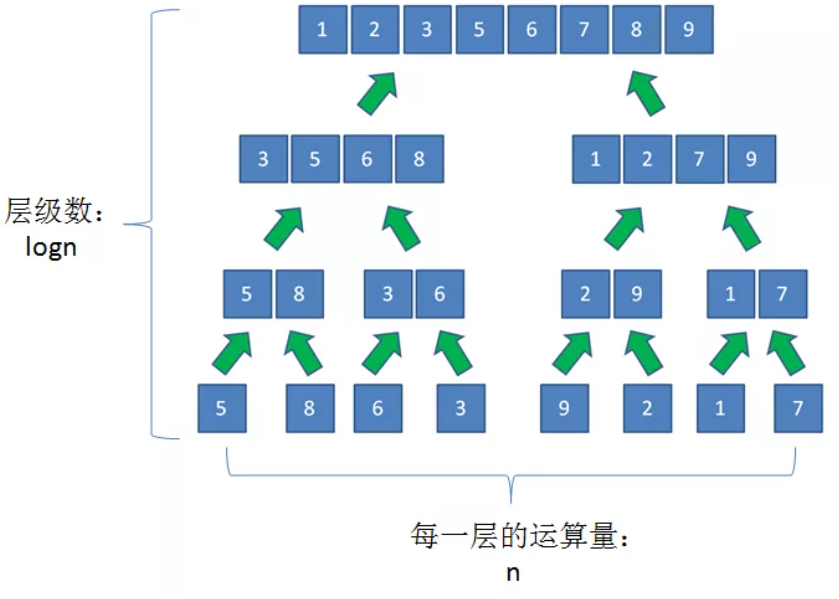
同一层的所有递归函数的运算总量为 n，树高为logn，因此时间复杂度为 O(nlogn)。同一层的所有递归函数使用的额外空间为n，总的额外使用空间为 nlogn，但是回到上一层递归时，下层递归的所有空间都已经释放，因此所有额外使用的空间不是叠加的，因此额外使用的空间最大值为n，空间复杂度为O(n)。

 

总结：归并排序复杂度为 O(nlogn)，空间复杂度为O(n)，而且是一个稳定的排序，不会出现相同值乱序的问题。

 

 

最后奉上所有排序的复杂度和优缺点归纳

根据时间复杂度可以将排序算法分为3个梯队。

 

O(n^2)的排序算法比较（冒泡排序、选择排序 和 插入排序）

从性能上看，冒泡排序和插入排序的元素比较交换次数取决于原始数组的有序程度。插入排序的性能略高于冒泡排序，因为冒泡排序在每轮排序中对所有未排序区内的元素进行比较和交换，插入排序只需在已排序区找到指定位置即可停止比较，不会对整个已排序区比较，而且挪动元素的成本低于交换元素。

选择排序的比较交换次数是固定的，和原始数组的有序程度无关。

因此，当原始数组接近有序时，插入排序性能最优；当原始数组大部分元素无序时，选择排序性能最优。

 

从稳定性看，冒泡排序和插入排序是稳定排序，值相同的元素在排序后仍然保持原本的先后顺序。选择排序是不稳定排序。

 

O(nlogn)的排序算法比较（快排、堆排序、归并排序）

从性能上看，希尔排序的平均时间复杂度最快可以达到O（n^1.3），性能略低于O(nlogn)。

快速排序的平均时间复杂度是O（nlogn），但是在极端情况下（两个分区中一个分区很多元素，一边分区很少元素），最坏时间复杂度是O（n^2）。

归并排序和堆排序的时间复杂度稳定在O（nlogn）。

堆排序比归并排序和快排的性能略低一些。主要是由于二叉堆的父子节点在内存中并不连续。根据CPU的空间局部性原理，CPU在每次访问数据的时候，会把内存中相邻的数据也一并存入缓存。这样一来，CPU以后再访问邻近的数据就不需要重新访问内存，而是访问CPU缓存，从而大大提升了程序执行的效率。因此堆排序的平均性能比快速排序和归并排序略低。

快速排序和堆排序是原地排序，不需要开辟额外空间。而归并排序是非原地排序，在merge操作的时候需要借助额外的辅助数组来完成。

 

从稳定性看，归并排序是稳定排序，快速排序和堆排序是不稳定排序。

 

线性复杂度排序算法比较（计数排序、基数排序和桶排序）

计数排序的时间复杂度是O（n+m），其中m是原始数组的整数范围。

桶排序的时间复杂度是O（n），这是在分桶数量是n的前提下。

基数排序的时间复杂度是O（k（n+m）），其中k是元素的最大位数，m是每一位的取值范围。

至于排序的稳定性，这三种排序算法都属于稳定排序。