· 二叉堆是什么

二叉堆从逻辑上来说是一个具有自动排序功能的二叉树（最大堆是栈顶为最大值，降序；最小堆是升序）；从物理上来说本质是一个数组。

 

二叉堆具有以下个特性（以升序的最小堆为例）：

1、它是一个完全二叉树（即除了最底下的两层，其他层的节点一定会有2个子节点），例如这就是一个完全二叉树

 

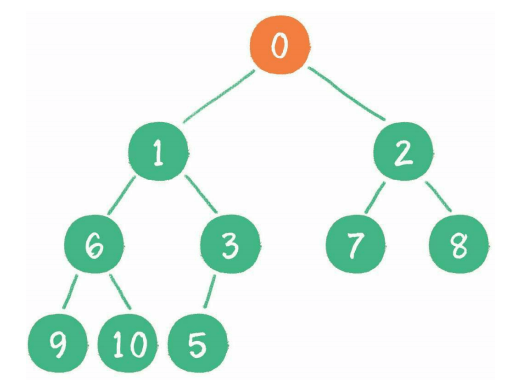
2、父节点的值总是小于（或等于）左右子节点的值

3、插入和删除一个节点时能够自动调节树，使其永远满足第二点

 

 

（最小）二叉堆基本操作

1、插入节点

插入节点永远是插入到最后一个节点并通过上浮操作到达合适的位置，如下所示：

 

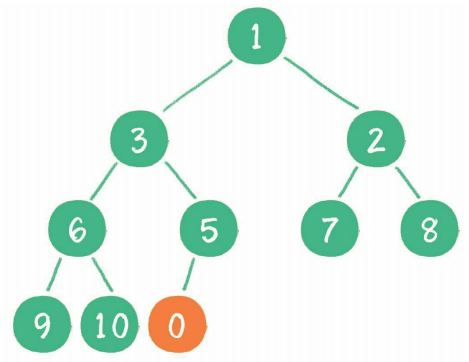
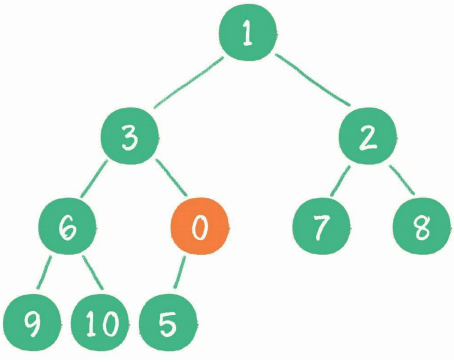
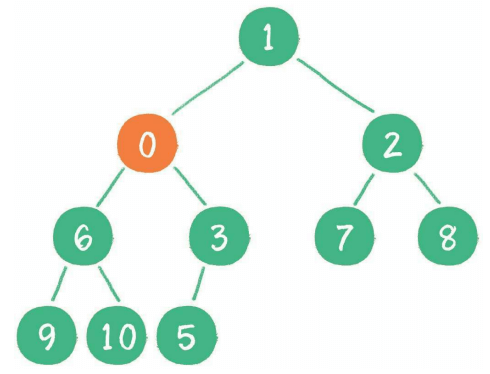
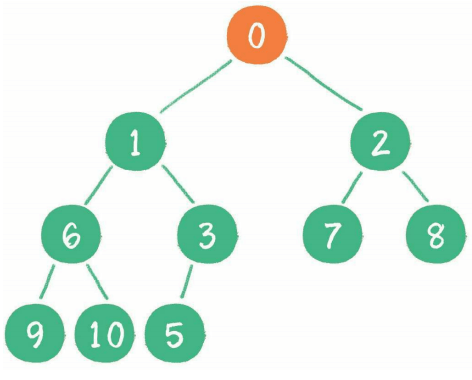
2、删除节点

二叉堆删除节点会删除根节点（一般不会删除非根节点外的节点），并且用最后一个节点放到根节点上占位，再将根节点下沉到特定位置

 

 

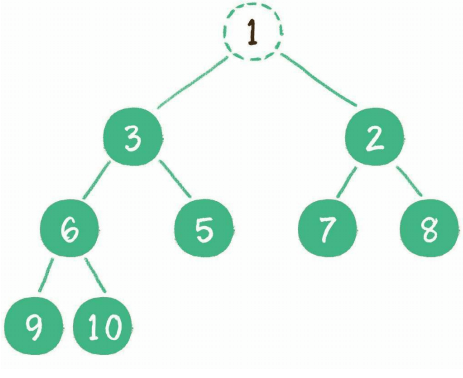
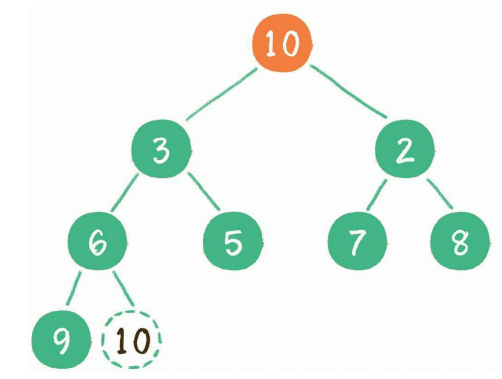
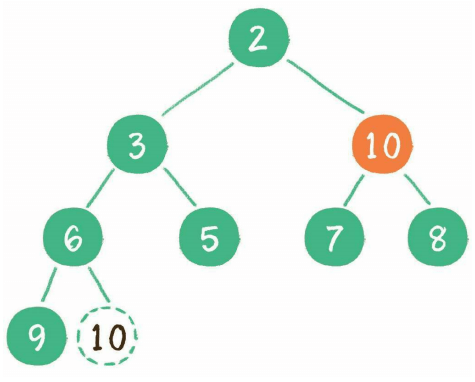
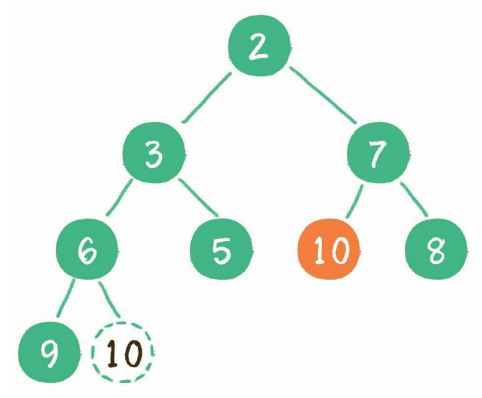
3、构建二叉堆

构建二叉堆需要先构建一个无序的完全二叉树后，再从最后一个有子节点的节点（即最后一个非叶子节点）开始，从下往上的对一个个节点依次做下沉操作

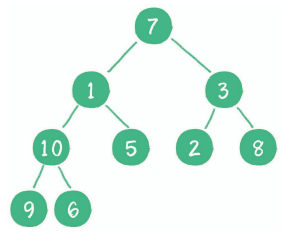
例如上图这个无序二叉树，需要依次对10,3,1,7这几个节点做下沉操作。

上浮和下沉的最大交换次数是树的层数，我们知道树的层数约等于树节点数量的取对数，所以上浮和下沉的复杂度是O(logn)。

二叉堆的构建需要对每个非叶子节点做下沉操作，每个下沉操作为O(logn)，表面看构建二叉堆的复杂度为O(nlogn)，但实际上全部节点下沉的整体复杂度是O(n)。

 

 

二叉堆一般使用顺序存储的数组作为底层结构。假设父节点的下标是parent，那么它的左孩子下标就是 2×parent+1；右孩子下标就是2×parent+2

 

下面是二叉堆的实现：

// 二叉堆
type Heap []int

// 最小堆上浮操作
func UpAdjust(heap Heap){
	childIdx := len(heap) - 1
	parentIdx := (childIdx - 1) / 2 	// 除成小数会向下取整
	temp := heap[childIdx]				// 临时变量记录要上浮的节点的值

	for childIdx > 0 && temp < heap[parentIdx]{		// 不要写成heap[childIdx] < heap[parentIdx]
		heap[childIdx] = heap[parentIdx]
		childIdx = parentIdx
		parentIdx = (childIdx - 1) / 2
	}
	heap[childIdx] = temp
}

// 最小堆下沉操作
func DownAdjust(heap Heap, idx int){	// 对指定下标的节点下沉
	if idx + 1 > len(heap){		// 超出范围的下标
		return
	}

	parentIdx := idx
	childIdx := parentIdx * 2 + 1	// 默认要替换的子节点取左节点
	temp := heap[parentIdx]

	for childIdx <= len(heap) - 1{	// 如果节点还没有下沉到超过堆长度的位置就可以继续做下沉操作
		// 取左右子节点中小的那个节点与temp比较
		if childIdx + 1 <= len(heap) - 1 && heap[childIdx] > heap[childIdx + 1]{
			childIdx++
		}

		if temp <= heap[childIdx]{
			break
		}
		heap[parentIdx] = heap[childIdx]
		parentIdx = childIdx
		childIdx = parentIdx * 2 + 1
	}
	heap[parentIdx] = temp	// 不要写成heap[parentIdx] = temp，不然会超出数组范围
}

// 下沉到指定下标操作
func DownAdjustToLastIdx(heap Heap, idx, lastIdx int){	// 对指定下标的节点下沉
	if idx + 1 > len(heap){		// 超出范围的下标
		return
	}

	parentIdx := idx
	childIdx := parentIdx * 2 + 1	// 默认要替换的子节点取左节点
	temp := heap[parentIdx]

	for childIdx <= lastIdx{	// 如果节点还没有下沉到超过堆长度的位置就可以继续做下沉操作
		// 如果有右节点而且右节点小于左节点，则取左节点替换
		if childIdx + 1 <= lastIdx && heap[childIdx] > heap[childIdx + 1]{
			childIdx++
		}

		if temp <= heap[childIdx]{
			break
		}
		heap[parentIdx] = heap[childIdx]
		parentIdx = childIdx
		childIdx = parentIdx * 2 + 1
	}
	heap[parentIdx] = temp	// 不要写成heap[parentIdx] = temp，不然会超出数组范围
}

// 构建最小二叉堆
func BuildHeap(arr []int) (heap Heap){
	heap = (Heap)(arr)
	lastIdx := (len(heap) - 2) / 2		// 最后一个节点下标

	for idx := lastIdx; idx >= 0; idx--{
		DownAdjust(heap, idx)
	}

	return heap
}

 

 

·优先队列

优先队列的本质是一个二叉堆，元素从一端入列，另一端出列。但和普通队列不同的是他不遵循先进先出，而是无论入队顺序如何，都是最大或者最小的元素优先出队。

 

有意思的是，优先队列并不是一个有序的队列（或者说不完全有序），但是将元素出列时是有序的出列。原因是优先队列逻辑上并不是一个线性数据结构，而是一个树形结构。

 

当有元素入列时，该元素会先进入队列尾部，并上浮到合适的位置。

当有元素出列时，实际上是获取堆顶（树的根节点）元素，该元素会被最后一个元素（最后一个叶子节点）替换，并下沉到合适的位置。

 

所以优先队列入列和出列的复杂度为O(logn)

 

下面是优先队列的代码实现

// (最小)优先队列

func InitPriorityQueue() *Heap{
	pq := make(Heap, 0, 32)	// 队列初始容量为32
	return &pq
}

// 入列
func EnQueue(pq *Heap, ele int){
	*pq = append(*pq, ele)
	UpAdjust(*pq)
}

// 出列
func DeQueue(pq *Heap) (target int){
	if len(*pq) == 0{
		panic("priority empty！")
	}
	target = (*pq)[0]

	// 切片的最后一个元素放到第一个元素
	(*pq)[0] = (*pq)[len(*pq) - 1]

	//再删除最后一个元素，切片的len会自动-1
	*pq = (*pq)[:len(*pq) - 1]

	// 对根节点做下沉操作
	DownAdjust(*pq, 0)

	return target
}