更多优质内容
请关注公众号
请关注公众号
·堆排序
堆排序顾名思义就是借助二叉堆进行排序。
如果需要升序排就用最大堆做堆排序
如果需要降序排就用最小堆做堆排序
回顾一下最大二叉堆的特性，最大二叉堆的顶端元素最大，而且父节点一定大于子节点。
那么如何使用最大堆做升序排序呢？
只需要不断让堆顶节点与未交换过的末尾节点交换， 并通过其自身下沉的特性让顶部元素到达合适的位置。让堆顶节点与未交换过的末尾节点交换就可以保证每一次交换后元素在树里面从右到左从下到上是有序的。
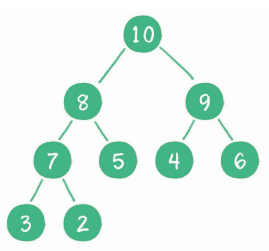
如下所示为一个未排好序的最大堆
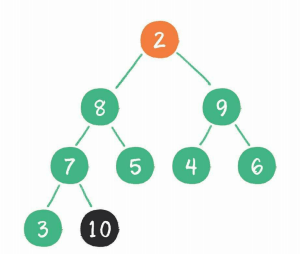
第一次交换（2和10）并下沉(2)
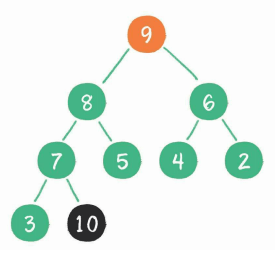
第二次交换（3和9） + 下沉（3）
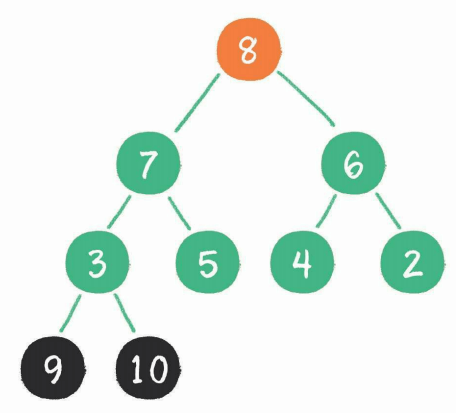
第三次交换（8和2） + 下沉（2）
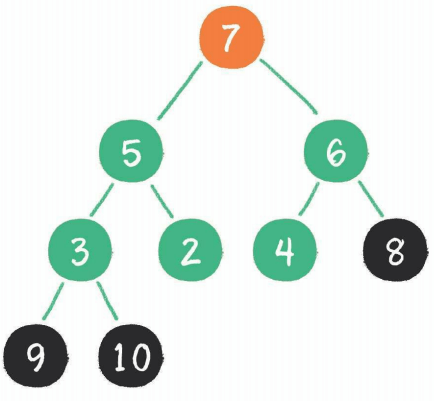
最终的结果是
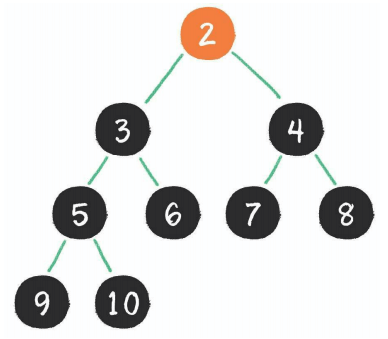
需要注意的是顶部元素不能下沉到已排好序（即黑色区域）的元素，只能下沉到未排好序的绿色区域。
代码实现如下：
func HeapSort(sl []int) (heap tree.Heap){
// 构建二叉堆
heap = tree.BuildHeap(sl)
temp := 0
// 交换顶部元素
for i:=len(heap) - 1; i > 0 ; i--{
temp = heap[i]
heap[i] = heap[0]
heap[0] = temp
// 再未排好序的区域内下沉
tree.DownAdjustToLastIdx(heap, 0, i-1)
}
return heap
}
// 下沉到指定下标操作
func DownAdjustToLastIdx(heap Heap, idx, lastIdx int){ // 对指定下标的节点下沉
if idx + 1 > len(heap){ // 超出范围的下标
return
}
parentIdx := idx
childIdx := parentIdx * 2 + 1 // 默认要替换的子节点取左节点
temp := heap[parentIdx]
for childIdx <= lastIdx{ // 如果节点还没有下沉到超过堆长度的位置就可以继续做下沉操作
// 如果有右节点而且右节点小于左节点，则取左节点替换
if childIdx + 1 <= lastIdx && heap[childIdx] > heap[childIdx + 1]{
childIdx++
}
if temp <= heap[childIdx]{
break
}
heap[parentIdx] = heap[childIdx]
parentIdx = childIdx
childIdx = parentIdx * 2 + 1
}
heap[parentIdx] = temp // 不要写成heap[parentIdx] = temp，不然会超出数组范围
}
该操作分为两步：构建堆（O(n)）和对n-1个元素进行下沉操作(O(nlogn))，所以该排序的时间复杂度为O(nlogn)。
