请关注公众号


树是一种非线性的数据结构,一棵树在逻辑上具有一个唯一的根节点,一个树节点在逻辑上具有多个指向其子节点的指针。
· 二叉树
二叉树就是每个节点只有两个分支的树。二叉树同样可以使用链表或者数组作为底层结构。
以链表为底层结构:
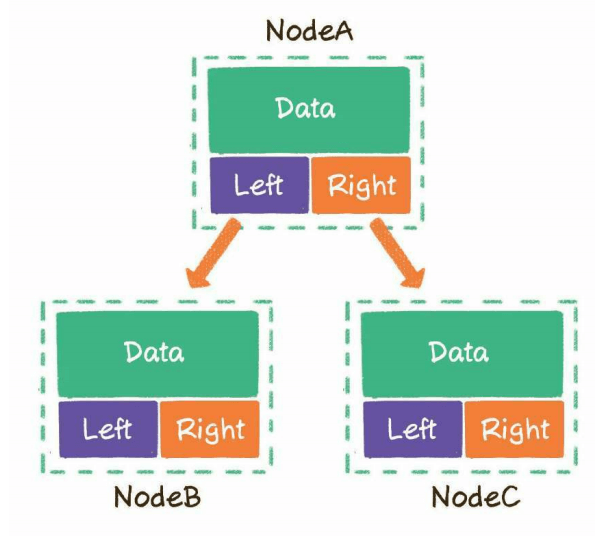
一个节点包含3部分
存储数据的data变量
指向左子节点的left指针
指向右子节点的right指针
使用链表表示树是直观的表示方式。
以数组为底层结构
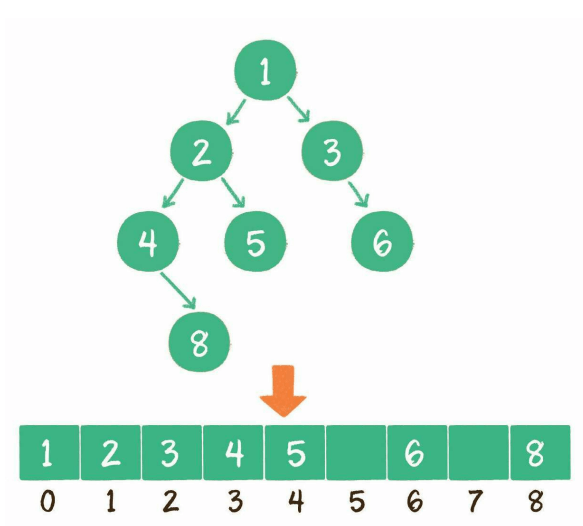
用数组作为底层结构的树具有如下规则:
对于一个满二叉树(就是树的每一个节点都有2个子节点或者没有子节点而不会只有一个子节点),它的所有节点可以填满数组没有空缺。但是对于非满二叉树,用数组为底层结构就会出现空缺,例如上面的数组下标5和下标7就会出现空缺。
所以对于一个稀疏的二叉树而言,使用数组是非常浪费空间的。
·二叉树的遍历
二叉树有3种深度优先遍历方式:前序遍历,中序遍历和后序遍历
1种广度优先遍历方式:层序遍历
前序遍历
中序遍历
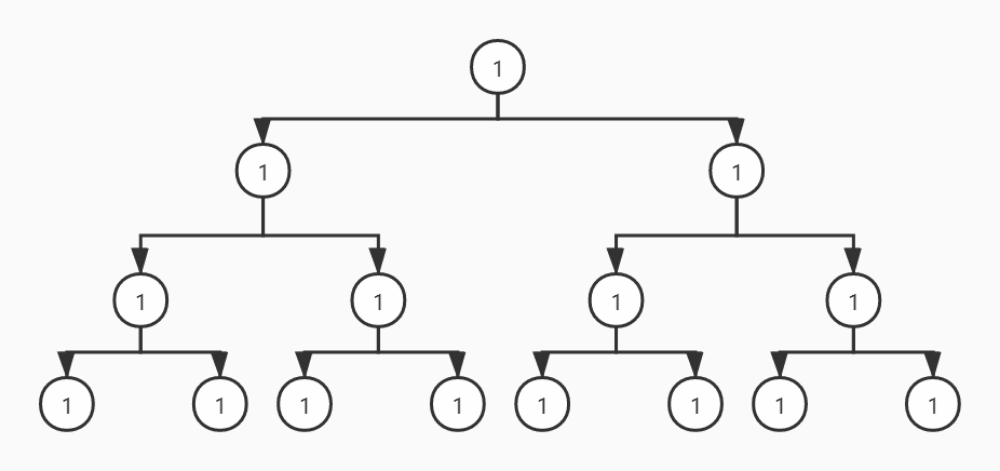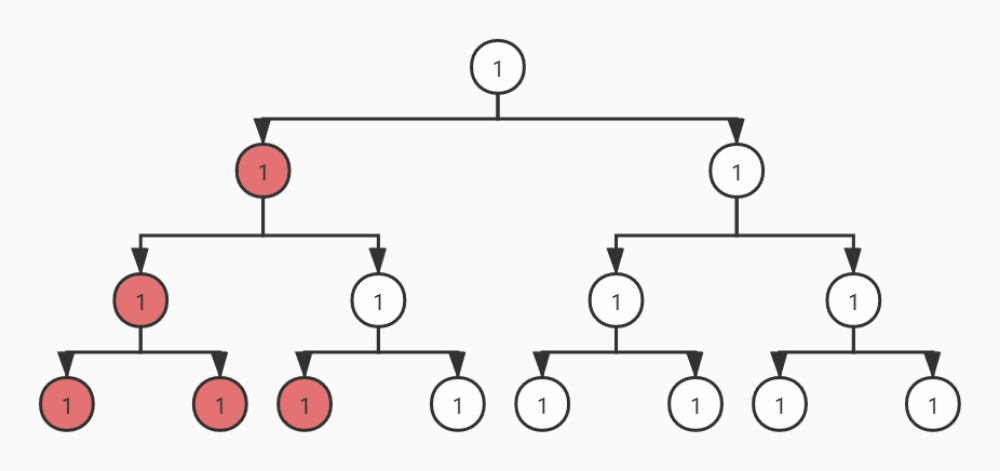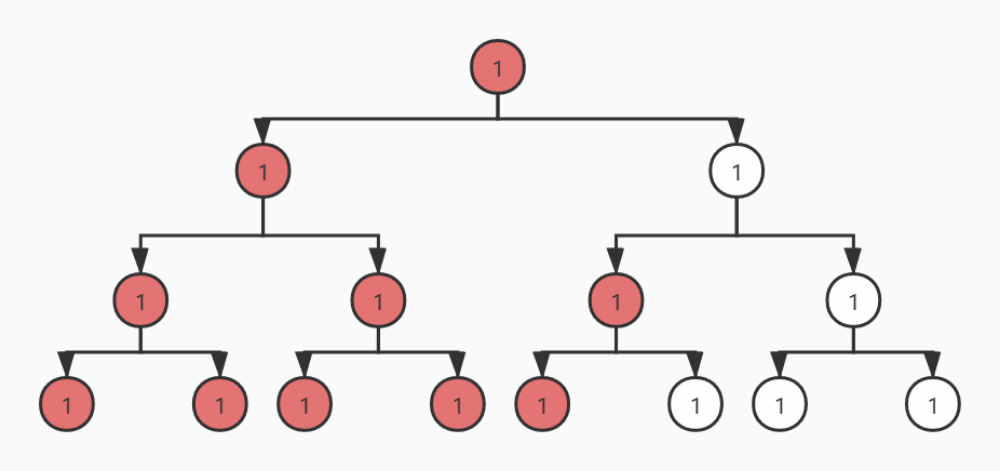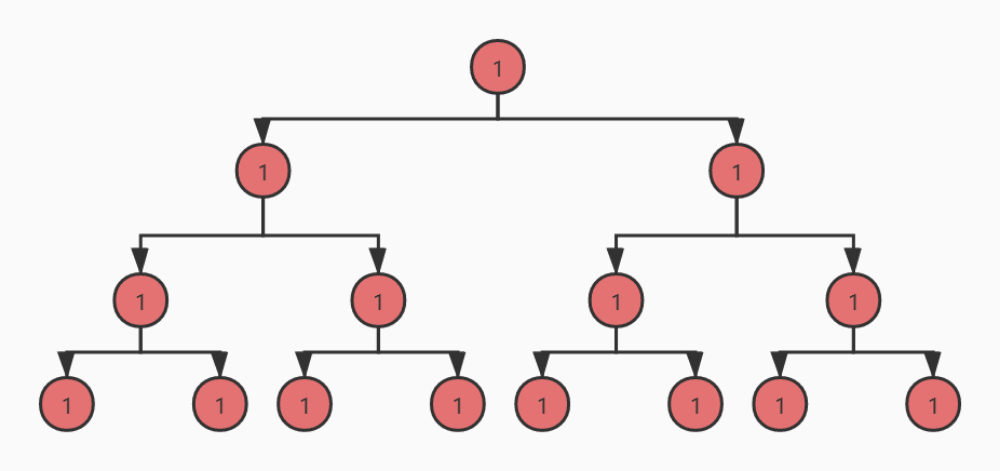
后序遍历
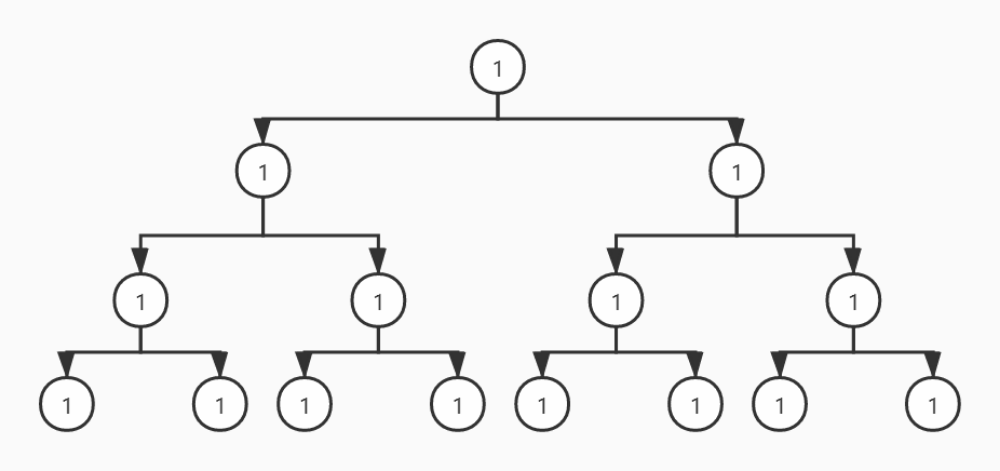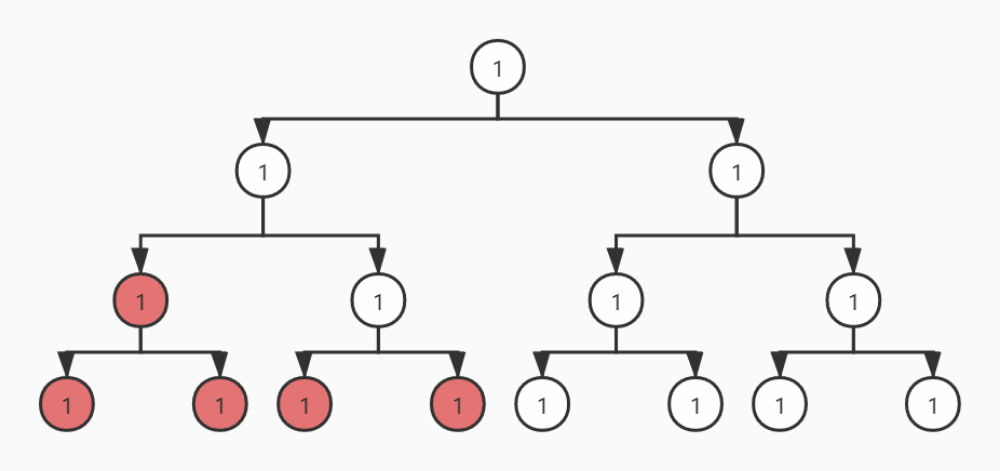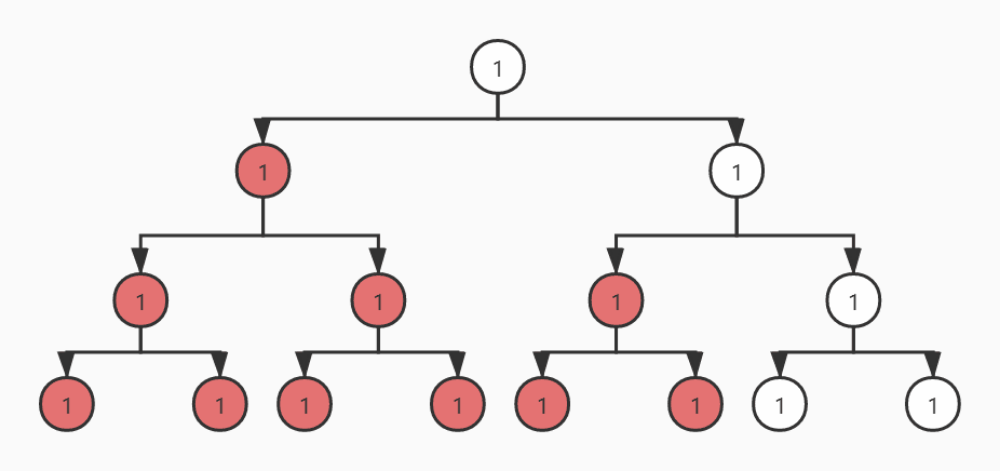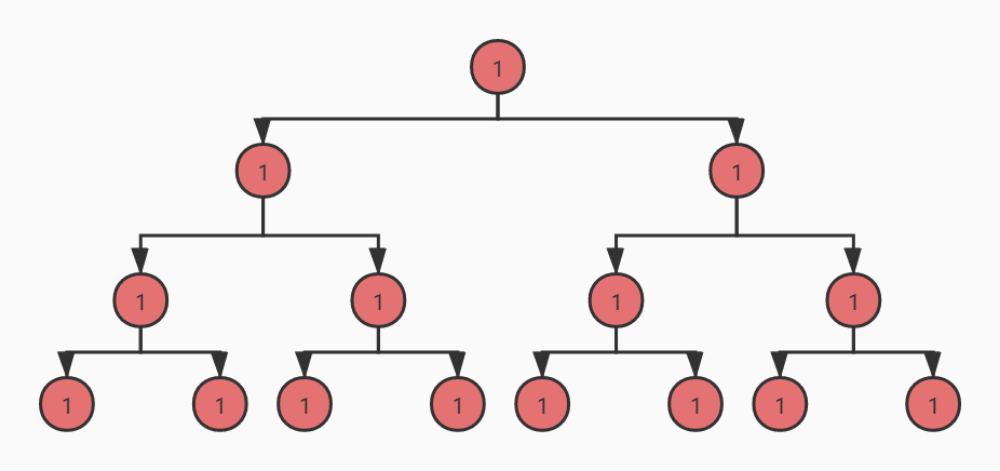
从动态图可以看出,前序遍历是自顶向下的遍历,中序和后序遍历是自底向上的遍历。
下面是3种遍历的实现(以GO实现):
package tree
import (
"fmt"
"zbp_struct/struct/list"
)
// 二叉树
type BTS struct{
LeftTree *BTS; // 左子树
RightTree *BTS; // 右子树
Val interface{}; // 根节点
}
// 前序遍历
func PreOrderTraveral(tree *BTS){
if(tree == nil){
return;
}
fmt.Println(tree.Val)
PreOrderTraveral(tree.LeftTree)
PreOrderTraveral(tree.RightTree)
}
// 中序遍历
func InOrderTraveral(tree *BTS){
if(tree == nil){
return;
}
InOrderTraveral(tree.LeftTree)
fmt.Println(tree.Val)
InOrderTraveral(tree.RightTree)
}
// 后序遍历
func PostOrderTraveral(tree *BTS){
if(tree == nil){
return;
}
PostOrderTraveral(tree.LeftTree)
PostOrderTraveral(tree.RightTree)
fmt.Println(tree.Val)
}
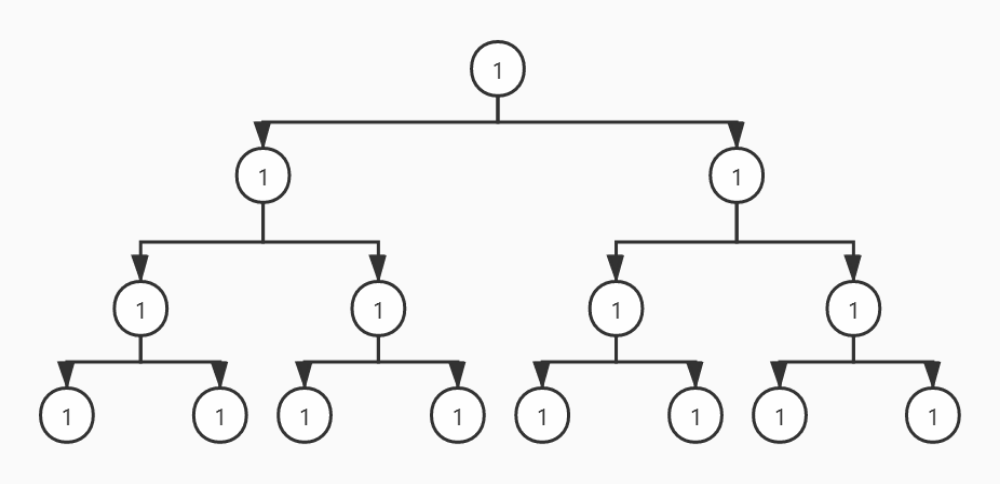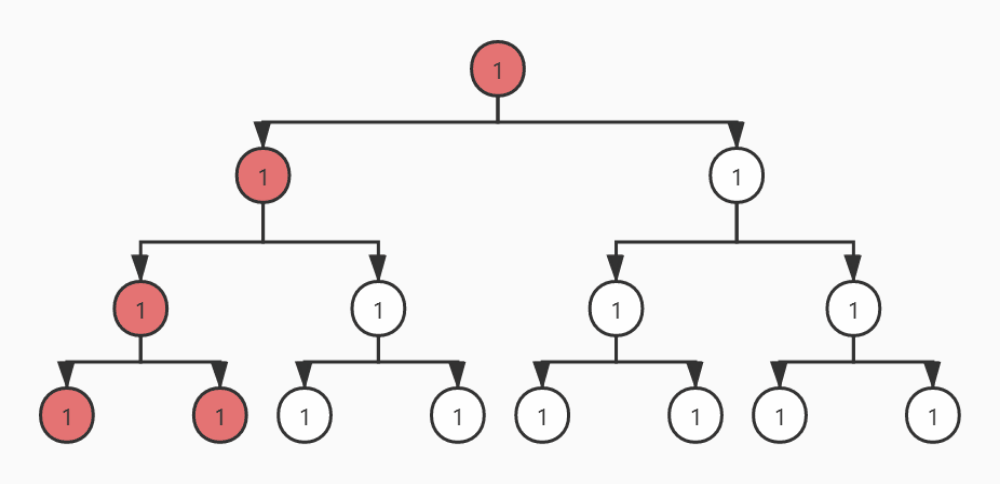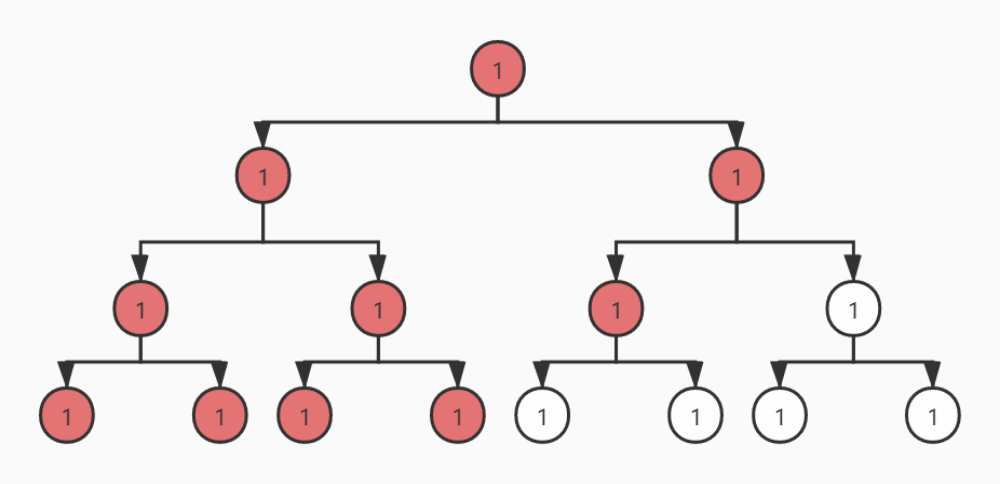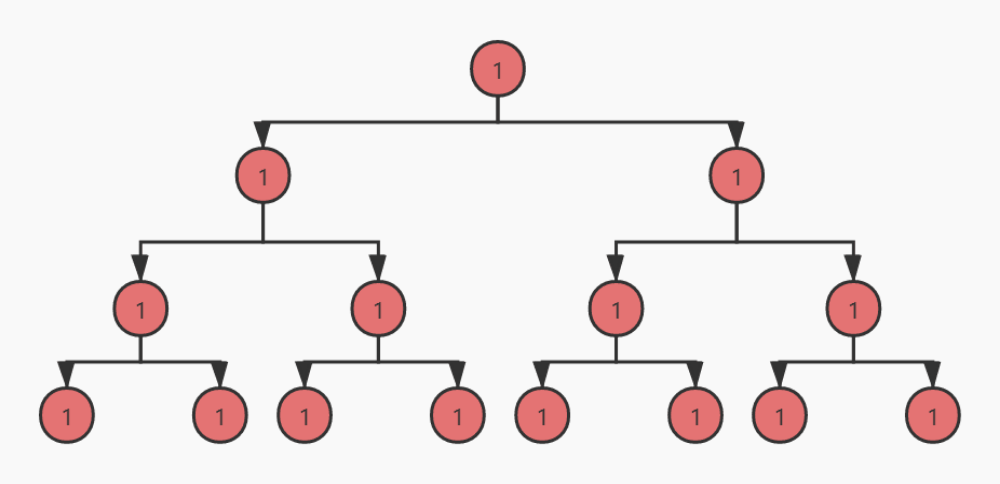
基本上,能用递归解决的问题都能用栈解决,只需借助栈和一个指针就能做到非递归前序遍历。栈存储的是遍历到当前节点的遍历路径(存的是树节点指针)。如下所示是一个前序遍历(借助栈)的过程:
节点4既没有左孩子,也没有右孩子,我们需要回溯到上一个节点2。栈已经存储了刚才遍历的路径。让旧的栈顶元素4出栈,就可以重新访问节点2,得到节点2的右孩子节点5。此时节点2已经没有利用价值(已经访问过左孩子和右孩子),节点2出栈,节点5入栈。
代码实现如下:
// 非递归版的前序遍历
func PreOrderTraveralWithStack(tree *BTS){
stack := list.InitLinkedList() // 使用单向链表模拟一个栈
curNode := tree // 当前遍历节点为根节点,curNode指针表示即将要入栈的节点
for curNode != nil || stack.Length > 0{ // 当前遍历节点如果为nil而且栈内没有可回溯的节点则表示遍历完所有节点
for curNode != nil{
fmt.Println(curNode.Val) // 输出当前节点值
stack.UnShift(curNode) // 记录当前遍历过的节点路径
curNode = curNode.LeftTree // 遍历下一个左节点,如果没有左节点则跳出第一层for循环并回溯;如果有左节点则重复该流程
}
//if(stack.Length > 0){
// 回溯
fNode := (stack.Shift()).(*BTS) // 弹出当前节点的父节点
curNode = fNode.RightTree // 以父节点的右节点作为当前遍历节点,并遍历该右节点的左子树
//}
}
}
非遍历版本的中序和后序遍历:
// 非递归版的中序遍历
func InOrderTraveralWithStack(tree *BTS){
stack := list.InitLinkedList() // 使用单向链表模拟一个栈
curNode := tree // 当前遍历节点为根节点
for curNode != nil || stack.Length > 0{ // 当前遍历节点如果为nil而且栈内没有可回溯的节点则表示遍历完所有节点
for curNode != nil{ // 如果当前节点有左子节点
stack.UnShift(curNode) // 记录
curNode = curNode.LeftTree // 查看其左子节点
}
// 如果上一个节点的左节点为nil则回溯
fNode := (stack.Shift()).(*BTS)
fmt.Println(fNode.Val)
// 开始往右子树遍历
curNode = fNode.RightTree
}
}
// 非递归版的中序遍历(需要用到两个栈)
func PostOrderTraveralWithStack(tree *BTS){
// 第一个栈放要遍历的根节点
stack1 := list.InitLinkedList()
stack1.UnShift(tree)
// 第二个栈放已经遍历了的节点,这个栈里面的存放的节点顺序(从栈顶到栈底)必须是左右中节点
stack2 := list.InitLinkedList()
for stack1.Length > 0 {
curNode := (stack1.Shift()).(*BTS)
if curNode.LeftTree != nil{ // 如果有左子树,就需要放到stack1以待遍历该左子树
stack1.UnShift(curNode.LeftTree)
}
if curNode.RightTree != nil{ // 右子树同理,不过必须是先放左子树后放右子树,因为我们要先遍历右子树后遍历左子树,先遍历的右子树节点先放到stack2,因此回溯stack2的时候就是左子树的节点比右子树节点先回溯
stack1.UnShift(curNode.RightTree)
}
// 将根节点放到stack2以待回溯
stack2.UnShift(curNode)
}
// 当遍历完所有树,开始回溯
for stack2.Length >0{
node := (stack2.Shift()).(*BTS)
fmt.Println(node.Val)
}
}
层序遍历
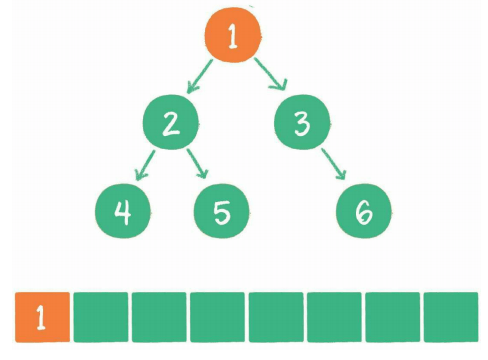
层序遍历是一种从上到下从左到右的遍历方式。该遍历方法需要用到一个队列,队列中存放要遍历的根节点,当该根节点取出时,它的左右子树就会入队。
过程如下
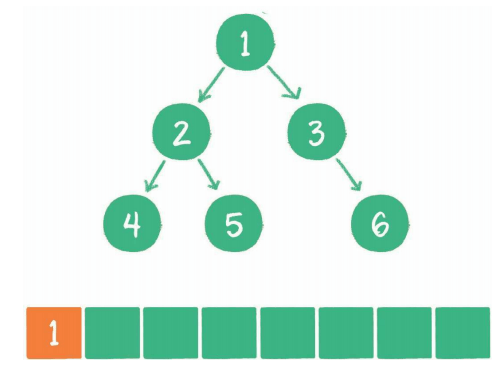
根节点1入列
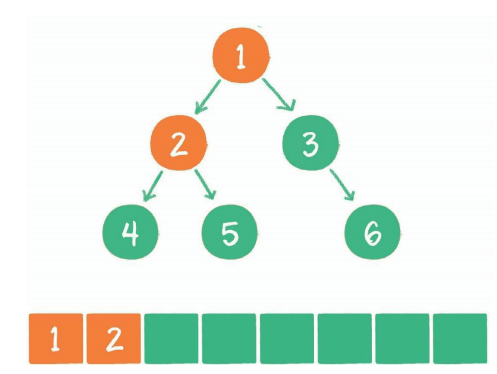
根节点1出队,它的左右子节点入队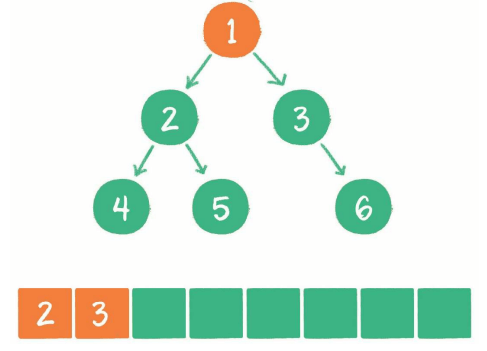
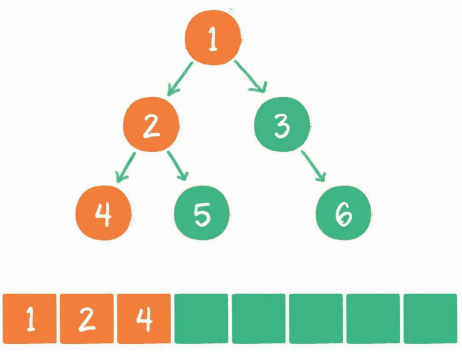
节点2出列,左右子节点45入列。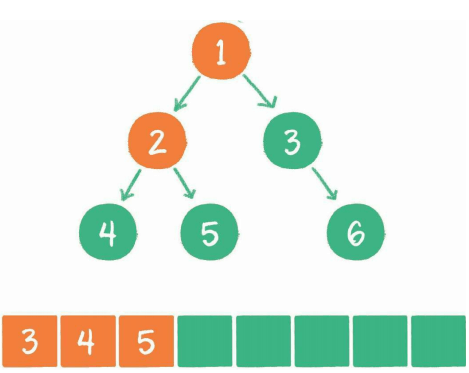
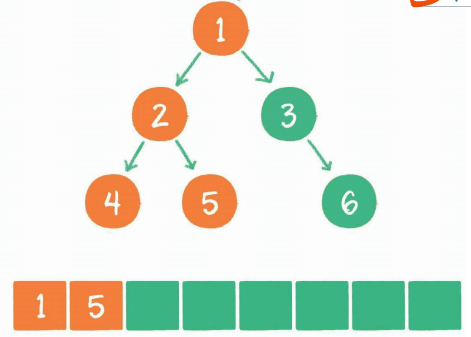
节点3出列,右子节点6入列
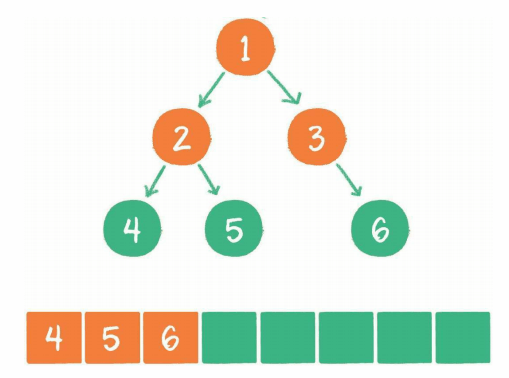
最后4、5、6没有子节点,依次出列
层序遍历代码实现
// 层序遍历(广度优先)
func LevelOrderTraveral(tree *BTS){
if tree == nil{
return
}
queue := list.InitLinkedList()
queue.Append(tree)
for queue.Length > 0 {
curNode := (queue.Shift()).(*BTS)
fmt.Println(curNode.Val)
if curNode.LeftTree != nil{
queue.Append(curNode.LeftTree)
}
if curNode.RightTree != nil{
queue.Append(curNode.RightTree)
}
}
}
· 根据数组或链表构建二叉树树
这是一个把线性结构变为非线性结构的过程,也可以分为深度优先(以前序遍历为例)或者广度优先(层序遍历)2种方式构建。
前序遍历构建二叉树
// 根据一个数组构建一个二叉树(以前序遍历的方式)
func CreateTreeFromArr(arr []interface{}) *BTS{
// arr = []interface{16, 14, 13, 10, nil, nil, 17, nil, nil, 15, nil, 19, nil, nil, 18, 6, nil, 27, nil, nil, 30, 29, nil, nil, nil}
if len(arr) == 0{
return nil
}
curIdx := 0
var createTreeFromArr func(curIdx int) (*BTS, int) // 定义一个闭包
createTreeFromArr = func(curIdx int) (*BTS, int){ // 前序遍历
if curIdx+1 >= len(arr) || arr[curIdx] == nil {
curIdx++
return nil, curIdx
}
node := InitTree(arr[curIdx])
curIdx++ // 移动当前数组指针
node.LeftTree, curIdx = createTreeFromArr(curIdx)
node.RightTree, curIdx = createTreeFromArr(curIdx)
return node, curIdx
}
root, _ := createTreeFromArr(curIdx)
return root
}
// 根据一个链表构建一个二叉树(以前序遍历的方式)
func CreateTreeFromList(inputList *list.LinkedList) *BTS{
if inputList == nil || inputList.Cur == nil || inputList.Length == 0{
return nil
}
// 使用前序遍历的方式构建这个树
if inputList.Cur.Val == nil{
inputList.Cur = inputList.Cur.Next
return nil // 如果未遍历完但是链表当前节点的值为nil,表示该分支到达叶子节点
}
// 以前序遍历的方式构建树
tree := InitTree(inputList.Cur.Val)
inputList.Cur = inputList.Cur.Next
tree.LeftTree = CreateTreeFromList(inputList)
tree.RightTree = CreateTreeFromList(inputList)
return tree
}
层序遍历构建二叉树
// 根据一个链表构建一个完全二叉树(以层序遍历的方式)
func CreateTreeFromListByLevel(inputList *list.LinkedList) (tree *BTS){
// []interface{}{16, 14, 18, 13, 15, 6, 30, 10, 17, nil, 19, nil, 27, 29, nil}
if(inputList == nil || inputList.Length == 0){
return tree
}
queue := list.InitLinkedList() // 使用一个队列记录已经进入树但是还没有分配左右子节点的节点
tree = InitTree(inputList.Cur.Val) // 将链表中的第一个节点放入树中作为根节点
queue.Append(tree) // 将根节点放入队列中记录起来
inputList.Cur = inputList.Cur.Next
var curNode *BTS // 定义一个树节点作为当前节点
for inputList.Cur != nil && queue.Length > 0{
curNode = (queue.Shift()).(*BTS) // 出列节点给他分配左右节点
if inputList.Cur.Val != nil{ // 如果链表节点的val为nil,那么对应的左节点为nil,如果没有这层判断就变成了有左节点但左节点的val为nil
curNode.LeftTree = InitTree(inputList.Cur.Val)
queue.Append(curNode.LeftTree)
}
inputList.Cur = inputList.Cur.Next
if inputList.Cur == nil{
break
}
if inputList.Cur.Val != nil {
curNode.RightTree = InitTree(inputList.Cur.Val)
queue.Append(curNode.RightTree)
}
inputList.Cur = inputList.Cur.Next
}
return tree
}
