计数排序

计数排序是一种需要额外空间存储，复杂度为线性复杂度(O(n))的排序方式。

 

基本思路

非线性复杂度的排序算法的思路是交换，而计数排序无需交换。假如一个序列的大小范围是[a, b]，可重复。它的长度为n。

需要一个长度为 b-a的数组，数组的下标就是序列中的元素的值，数组的值是序列中该元素的出现次数，例如arr[23]存放的是序列中23这个数的出现次数。我们需要遍历这个序列，并将序列中元素出现的次数填入到这个数组。最后再遍历这个数组覆盖原有序列即可。

 

 

例如：

9，3，5，4，9，1，2，7，8，1，3，6，5，3，4，0，10，9 ，7，9

 

它的最大值和最小值范围是 0~10。所以需要一个0~10的数组：

 

代码实现如下：

func CountSort(sl []int) []int{
	maxVal := sl[0]
	minVal := sl[0]
	for i:=1; i<len(sl); i++{
		if sl[i] > maxVal{
			maxVal = sl[i]
			continue
		}

		if sl[i] < minVal{
			minVal = sl[i]
		}
	}

	container := make([]int, maxVal-minVal+1)
	idx := 0
	for i:=0; i<len(sl); i++{
		idx = sl[i] - minVal
		container[idx]++
	}

	curSlIdx := 0
	for i:=0; i<len(container); i++{
		for j:=0; j<container[i]; j++{
			sl[curSlIdx] = i + minVal
			curSlIdx++
		}
	}
	return sl
}

如果原始数列的长度是n，最大和最小整数的差值是m，则空间复杂度为O(m)。时间复杂度为O(n+m)。

该算法的局限性比较大，首先仅能用于整数，因为中间容器的数组下标只能是整数。而且当最大和最小整数的差值过大的情况下，即使n很小，它的时间复杂度和空间复杂度也会很高。比如序列只有两个元素0和1亿。此时中间容器的长度会长达1亿。

 

上述计数排序是一个不稳定的排序，即相同的数可能出现乱序。如下所示：

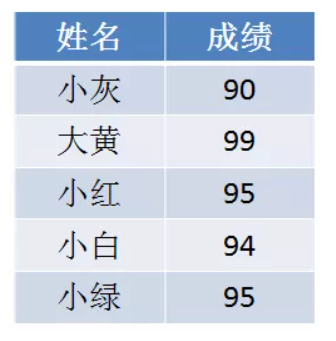
如果对这样的一个成绩排序，要求相同分数的同学的排序需要按照原榜单的顺序排序，上面的计数排序是办不到的。对此我们可以将计数排序优化。原本排序结果容器 container[i] 记录的是值 i 在原数组arr 的出现次数，现在变成 container[i]记录的是 值i 在原数组arr的排序后位置。

 

原本排序结果容器 container[i] 记录的是值 i 在原数组arr 的出现次数

 

现在变成 container[i]记录的是 值i 在原数组arr的排序后位置

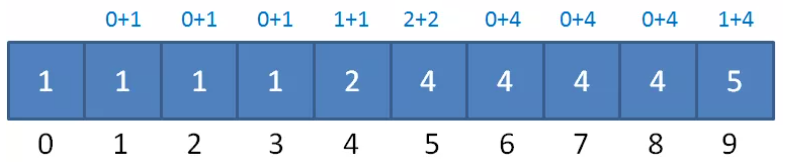
其中 container[0] = 1表示 90分 应该排在第一个位置，container[4] = 2 表示 94分应该排在第二个位置，container[5] = 4 表示 95分有2个，最后一个95分应该排在第四个位置。

 

得到这样的container数组之后，需要再创建一个空的输出数组 sortArray，需要从后往前遍历 原数组arr，container[arr[i].成绩]就是 arr[i] 在 sortArray的位置，并且每访问一次container[arr[i].成绩]，都需要将其减1，这样的话下一个分数相同的同学在sortArray的位置也会减1。

 

稳定版的计数排序代码实现如下：

type stu struct{
	name string		// 学生名字
	score int		// 成绩
}
func CountSort2(sl []*stu) []*stu{
	min := sl[0].score
	max := sl[0].score

	for i:=0; i<len(sl); i++{
		if sl[i].score < min{
			min = sl[i].score
		}
		if sl[i].score > max{
			max = sl[i].score
		}
	}

	container := make([]int, max - min + 1)
	for i:=0; i<len(sl); i++{
		idx := sl[i].score - min
		container[idx] += 1    //此时 container[idx] 是arr元素出现的次数
	}
	//sum := 0	// sum是排序位置
	for i:=1; i<len(container); i++{
		container[i] += container[i-1]    //此时 container[i] 是arr元素的排序位置
	}

	res := make([]*stu, len(sl))

	// 倒序遍历sl
	for i:=len(sl)-1; i>=0; i--{
		res[container[sl[i].score-min]-1] = sl[i]
		container[sl[i].score-min]--
	}
	return res
}

func TestCountSort(t *testing.T){
	score := []int{90,99,95,94,95,93,90,97,99}
	name := []string{"a","b","c","d","e","f","g","h","i"}
	arr := make([]*stu,len(score))
	for i, _ := range(score){
		arr[i] = &stu{name:name[i], score: score[i]}

	}
	res := CountSort2(arr)		// a g f d c e h b i
	for _, v := range(res){
		fmt.Println(v)
	}
}

 

 

基数排序

基数排序是在计数排序的基础上的一种排序，基数排序支持比计数排序更多的适用场景。

 

例如，为一组单词排序

banana

apple

orange

peach

cherry

........

........

基数排序的思路是对所有字符串按第最低位字符按照稳定版本的计数排序法排序（假设所有要排序的字符串长度相同），再按倒数第二低位字符排序，直到对第一位字符排序即可完成对所有字符串的排序。如果字符串的长度不尽相同，则往字符串低位补零使得所有字符串长度相同。

 

假设arr中最长字符串长度为k，则需要进行k轮稳定版计数排序。

之所以从后往前排序，是为了是高位字符相同的字符串再按较低位排序。

 

代码实现：

func RadixSort(arr []string) []string{
	// 不直接对arr内的字符串补0，否则还需要在返回结果前，将0给删掉
	// 获取arr中最长字符串的长度
	k := 0
	for _, s := range(arr){
		if len(s) > k{
			k = len(s)
		}
	}
	k--		// 上面的k记录的是arr中最长字符串的长度，k--才是最长字符串的最后一位的位置

	asciiLen := 128
	tmpArr := make([]string, len(arr))	// 存放每轮排序的临时结果，一轮排序就是按第k位字符排序，一个需要进行k轮排序
	for ; k >= 0; k--{	// 对arr中的字符串从低位到高位逐次用计数排序
		container := make([]int, asciiLen)

		// 获取统计数组
		for i:=0; i<len(arr); i++{
			charIdx := GetCharIndex(arr[i], k)
			container[charIdx]++
		}

		// 获取排序位置数组
		for i:=1; i<len(container); i++{
			container[i] += container[i-1]
		}

		// 倒序遍历arr得到tmpArr的值，tmpArr是本轮排序的临时结果
		for i:=len(arr)-1; i>=0; i--{
			charIdx := GetCharIndex(arr[i], k)
			tmpArr[container[charIdx]-1] = arr[i]
			container[charIdx]--
		}

		// 用tmpArr覆盖arr
		arr = append(arr[:0], tmpArr...)
	}
	return arr
}

func GetCharIndex(s string, k int) byte{	// 获取字符串 s 的第k位字符, k从0开始
	if k >= len(s){		// 如果 k 溢出s的长度，则返回0，相当于间接补0
		return 0	// 0的ascii码刚好是0
	}
	return s[k]
}

 

假设arr长度为n，arr中最长字符串长度为k，m是单个字符的取值范围（即最大字符和最小字符的差值，在本例中m=128）。每轮计数排序的时间复杂度为O(n+m)，k轮的时间复杂度为O(k(n+m))。空间复杂度为O(n+m)。

 

因此，基数排序的时间复杂度为 O(k(n+m))，空间复杂度为O(n+m)。由于k是一个常数，因此基数排序是一个线性级别的排序。

 

桶排序

桶排序是计数排序的优化，计数排序的中间容器的每个下标只能代表一个元素。而桶排序的一个桶代表一个区间范围。

 

该算法的性能取决于序列元素是否是均匀排布（例如 1 2 10 7 100 1000 10000就是一个不均匀的序列，总体区间为[1, 10000]但元素都会集中在前面的区间）。

 

Q1：桶的个数如何定？

一般以元素个数作为桶的数量，最后一个桶必须只包含最大的元素。每一个桶是一个一维数组，所有桶就是一个二维数组。

 

Q2：每个桶的区间范围如何定？

桶的区间 = (最大值 - 最小值) / (桶个数-1)。因为最后一个桶已经被最大元素占用，因此其他值只能均分到剩余的桶，所以分母为（桶个数-1）。平均一个桶放1个元素。

每一个桶都是左闭右开，第一个桶的左边界是序列中的最小值。

 

Q3：如何判断某个元素arr[i]位于哪个桶？

我们可以把[min, max)看做是一段总路程(总路程为 max - min，min为起点，max为终点)，arr[i]看做是路程中的某个点。因此只需计算arr[i]为与这段路程的占比 p = (arr[i] - min) / (max - min)。arr[i] 所位于的桶的序号 = math.floor(p * （桶的个数-1）)。需要注意最后一个桶已经被max元素占用，所以公式里是桶的个数-1。

所以 idx =  math.floor((arr[i] - min) / (max - min) * （桶的个数-1）) 就是桶的下标。

 

另一种算法就是 idx = math.floor((arr[i] - min) / range)，range是每个桶区间的长度。

 

如下所示：

对于这个序列

4.5，0.84，3.25，2.18，0.5

它最终会这样分布在桶里面

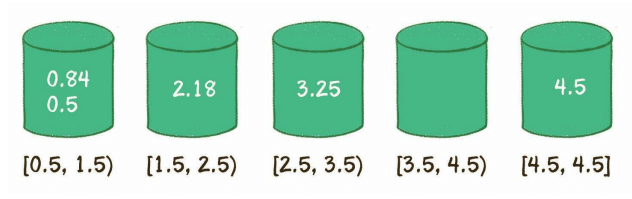
然后我们需要对每一个桶中的元素再排序（使用快排等性能高的排序）。

最后遍历所有的桶输出所有元素。

type Bucket []float64
func BucketSort(sl []float64) []float64{
	// 获取最大最小值
	maxVal := sl[0]
	minVal := sl[0]
	for i:=1; i<len(sl); i++{
		if sl[i] > maxVal{
			maxVal = sl[i]
			continue
		}

		if sl[i] < minVal{
			minVal = sl[i]
		}
	}

	// 创建桶列表
	bucketNum := len(sl)
	bucketList := make([]Bucket, bucketNum)
	areaRange := (maxVal - minVal) / (float64(bucketNum) - 1)

	// 往桶里面填充元素
	var bucketIdx int
	for i:=0; i<len(sl); i++{
		bucketIdx = int(sl[i] / areaRange) - 1	// 根据元素值计算他该放到哪个桶，bucketIdx需要定义为整数，这样的话除法会自动向下取整
		bucketList[bucketIdx] = append(bucketList[bucketIdx], sl[i])
	}

	// 对桶里的每个元素排序
	curSlIdx := 0
	for i:=0; i<len(bucketList); i++{
		sort.Float64s(bucketList[i])	// 使用go中的排序功能

		// 覆盖原数组
		for j:=0; j<len(bucketList[i]); j++{
			sl[curSlIdx] = bucketList[i][j]
			curSlIdx++
		}
	}

	return sl
}

该算法的复杂度贡献如下：

寻找最大最小值：O(n)

往桶填充元素：O(n)

桶内每个元素做排序：在元素相对均匀的情况下，运算量之和为n，所以复杂度是O(n)。

覆盖原数组：O(n)

 

所以总体的复杂度为O(n)。

考虑极端情况：如果所有的元素都集中在一个桶中（或者分布极不均匀的情况下），则会退化为O(nlogn)。因此桶排序适用于元素分布较均匀的场景下。

 

相比于快排这种O(nlogn)复杂度的排序（其空间复杂度为O(1)），计数排序和桶排序是牺牲了空间复杂度达到O(n)的时间复杂度(其时间复杂度为O(n)或者更大)。