先提出一个问题，如果让一个有序链表像有序数组使用二分查找一样实现高效查找。

 

· 跳表

跳表是一个具有多层索引的有序链表，借助索引可以像有序数组一样实现高效增删查操作。

 

跳表的特点如下

1、跳表由多层有序链表组成，每个链表节点具有上下左右4个方向的指针，上层索引和下层索引通过上下指针链接。

2、除了最底层链表存储原数据之外，其他上层链表都是索引链表，每一个上层链表都存放着下层链表的索引。

3、每插入一个节点都要从底层链表插入，并有50%的几率以该节点为索引建立它的上层索引，因此上层链表的节点数是下层链表节点的一半，在上层索引链表中查找目标节点所需的访问次数也可以比下层减少一半。

层数为 i，则该层的节点数为 n/(2^(i-1)) 。

4、跳表只存储最上层链表的头尾节点，所以查找时只能从上层链表先往右再往下找目标节点，增删时从上而下找到位于底层的目标节点，再自下而上多次插入和删除目标节点以及它的索引。

 

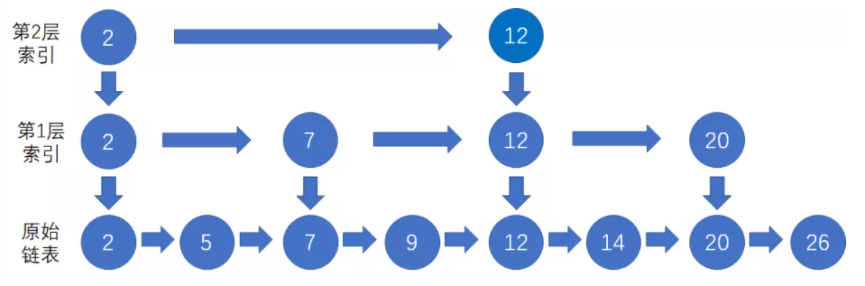
由于跳表在横向有多个节点，在纵向也有多层节点，因此在形状上类似一个二维数组，增删查时需要使用两层循环，外层循环决定层数，内层循环决定找到该层的第几个节点。

 

如果说在单层链表遍历一个节点是在一维的世界中水平的遍历一条链表，那么在跳表遍历一个节点就是在二维的世界中向右下方遍历一条链表。

 

· 跳表的增删查操作

下面是一个在跳表中查找20所在节点的例子：

1、先从顶层索引链表节点的第一个节点2开始往右查找，找到小于等于20且离20最近的索引节点12。

 

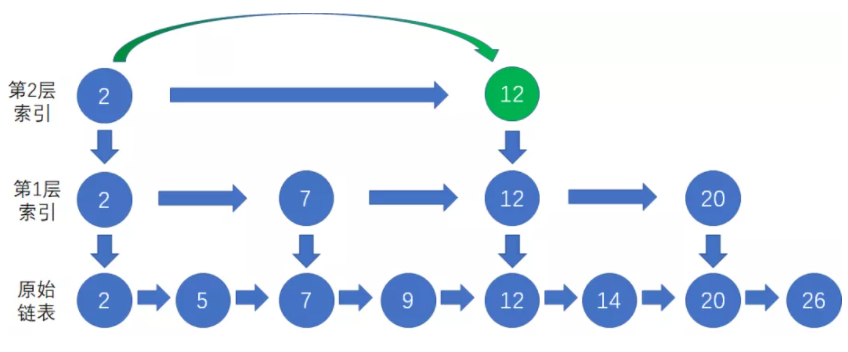
2、进入下层链表，在第1层索引链表中从索引节点12向右找到小于等于20且离20最近的索引节点20。

 

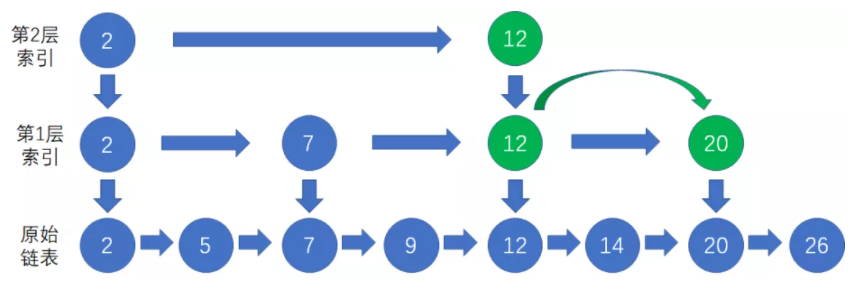
3、再进入下层链表，在原始链表（第0层）中从数据节点20开始向右找到等于20的节点。

 

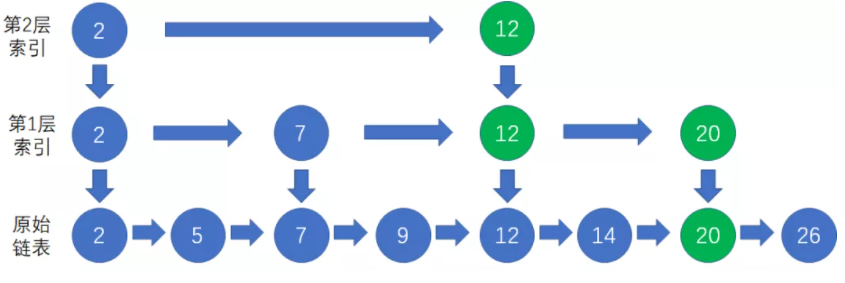
下面是一个在3层跳表中插入节点10的例子：

1、先自上而下对要插入的目标值10进行查询，在底层链表找到小于等于10且离10最近的数据节点，也就是节点9作为前置节点：

 

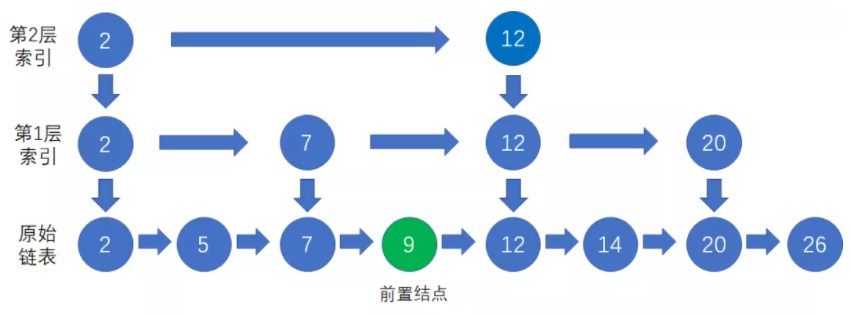
2、创建新节点10，插入到节点9后面：

 

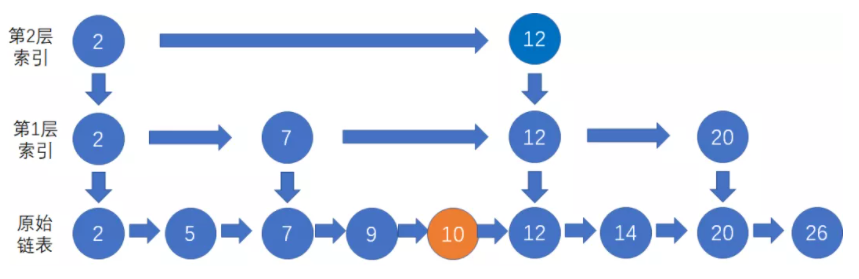
3、按照节点插入时有 50% 几率作为索引创建上层节点的规则，假设节点10成功晋升到第3层索引（即第4层链表），此时跳表的最高层数变为4层。

 

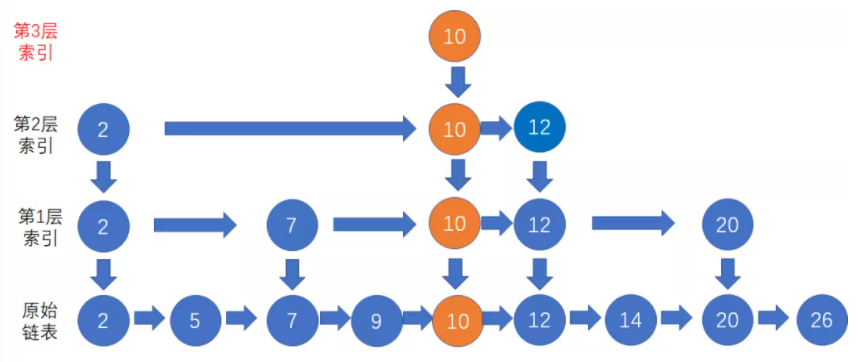
插入过程如上所示是一个先自上而下查找到目标插入位置，再自下而上插入原数据和索引的过程。

 

下面是一个在4层跳表中删除节点10的例子：

1、先自上而下对要删除的节点10进行查询，找到其底层节点

 

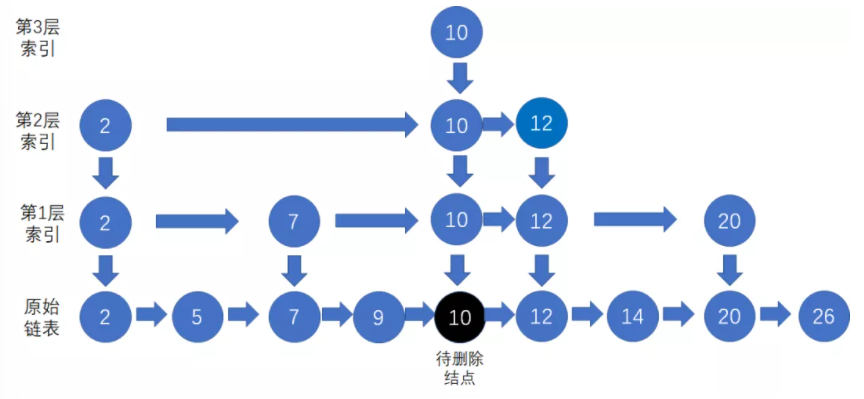
2、在自底向上删除每一层节点10（包括底层的原数据节点和上层的索引节点）：

 

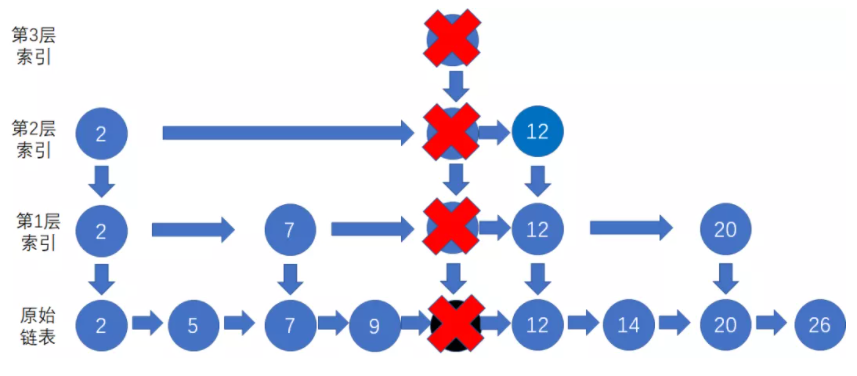
3、如果某一层索引的节点被删光，则删掉这一层链表：

 

 

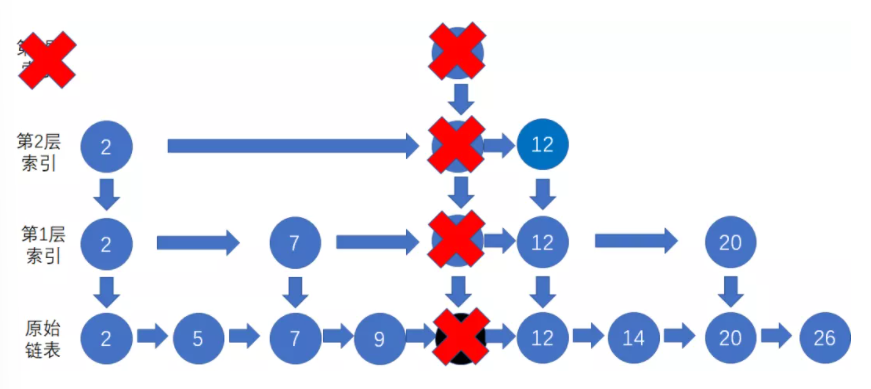
· 跳表的实现

1、跳表在实际实现时使用双向链表；

2、每一层链表都有一个value为负无穷的虚拟头结点 和 正无穷的虚拟尾结点，所有数值正常的节点都在虚拟头结点和尾结点之间。

 

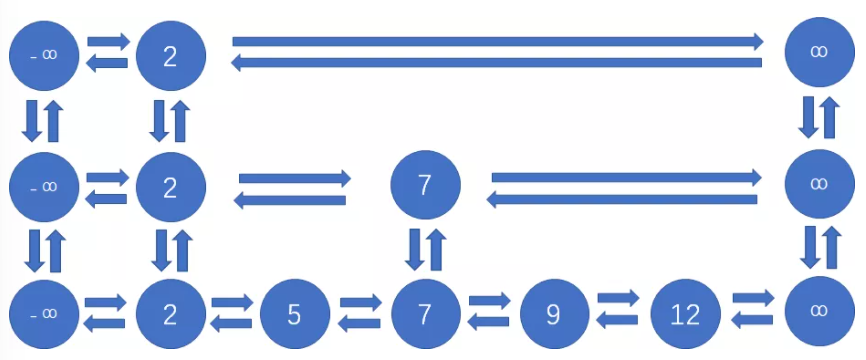
代码实现如下：

- 跳表结构

var skipListMaxLevel = 32	// 限定跳表的最大高度为32

// 跳表节点
type SkNode struct{
	left,right,up,down *SkNode
	Value int
}

func InitSkNode (value int) *SkNode{
	return &SkNode{Value: value}
}

// 跳表（假设跳表中的每个值都是唯一的）
type SkipList struct {
	head, tail *SkNode
	maxLevel	int
}

func InitSkipList() *SkipList{
	rand.Seed(time.Now().UnixNano())
	head := InitSkNode(math.MinInt32)
	tail := InitSkNode(math.MaxInt32)
	head.right = tail
	tail.left = head
	return &SkipList{
		head: head,
		tail: tail,
		maxLevel: 1,
	}
}

 

- 查询某个节点

func (this *SkipList) Search(data int) *SkNode{
	targetNode := this.searchNearestNode(data)
	if targetNode.Value == data{
		return targetNode
	}
	return nil
}

// 寻找某个data的位置，如果存在该data则返回该data的底层节点，不存在则返回比data小但离data最近的底层节点
func (this *SkipList) searchNearestNode(data int) *SkNode{
	curNode := this.head
	curLevel := this.maxLevel
	for curLevel > 1 {	// 该层循环负责纵向查找
		for curNode.right.Value <= data{	// 该层循环负责横向查找
			curNode = curNode.right
		}
		curNode = curNode.down	// 往下层链表找
		curLevel--
	}

	// 此时当前指针到达最底层，即curLevel == 1
	for curNode.right.Value <= data{
		curNode = curNode.right
	}
	return curNode
}

 

- 插入某个值

func (this *SkipList) Insert(data int) *SkNode{
	// 找到data要插入的位置
	prevNode := this.searchNearestNode(data)
	if prevNode.Value == data{	// 已经存在data
		return nil
	}

	// 在最底层插入节点
	insertNode := InitSkNode(data)
	this.insertAfter(prevNode, nil, insertNode)
	downNode := insertNode
	originInsertNode := insertNode	// 插入到底层的节点，即要返回的节点

	curLevel := 1		// 已经插入的层
	for curLevel < skipListMaxLevel && rand.Intn(2) == 1{
		prevNode = this.findPrevInLastLevel(prevNode, curLevel)	// 寻找已经插入的层的上一层的前置节点

		insertNode = InitSkNode(data)
		if curLevel+1 > this.maxLevel{	// 如果要插入的层比当前最大层数大
			this.createLevel(insertNode, downNode)
		}else{
			this.insertAfter(prevNode, downNode, insertNode)
		}
		downNode = insertNode
		curLevel++
	}
	return originInsertNode
}

// 在本层链表中往 prevNode 后插入节点 insertNode
func (this *SkipList) insertAfter(prevNode, downNode, insertNode *SkNode){
	insertNode.left = prevNode
	insertNode.right = prevNode.right
	prevNode.right.left = insertNode
	prevNode.right = insertNode

	if downNode != nil{	// 如果insertNode插入的位置不在第1层，则还要将其向下指针指向下层节点
		insertNode.down = downNode
		downNode.up = insertNode
	}
}

// 寻找上一层的前置节点
func (this *SkipList) findPrevInLastLevel(prevNode *SkNode, curLevel int) *SkNode{
	if curLevel != this.maxLevel{ // 如果本层已经是最高层，则不存在上一次的 prevNode
		for prevNode.up == nil{
			prevNode = prevNode.left
		}
		prevNode = prevNode.up
		return prevNode
	}
	return nil
}

// 创建最高层，并将insertNode插入到最高层中
func (this *SkipList) createLevel(insertNode, downNode *SkNode){
	newHead := InitSkNode(math.MinInt32)
	newTail := InitSkNode(math.MaxInt32)

	// 在上下方向连接头尾节点
	newHead.down = this.head
	newTail.down = this.tail
	this.head.up = newHead
	this.tail.up = newTail

	// 上下方向连接 insertNode和downNode
	insertNode.down = downNode
	downNode.up = insertNode

	// 在左右方向连接 头节点 - insertNode - 尾结点
	newHead.right = insertNode
	insertNode.right = newTail
	insertNode.left = newHead
	newTail.left = insertNode

	this.head = newHead
	this.tail = newTail
	this.maxLevel++
}

 

- 移除一个节点

func (this *SkipList) Remove(data int) *SkNode{
	// 找到data的位置
	deleteNode := this.searchNearestNode(data)
	if deleteNode.Value != data{	// 不存在要删除的data
		return nil
	}
	originDeleteNode := deleteNode

	curLevel := 1
	for deleteNode != nil{
		nextDeleteNode := deleteNode.up		// 记录下一个要删除的节点
		deleteLevel := curLevel > 1 && deleteNode.left.Value == math.MinInt32 && deleteNode.right.Value == math.MaxInt32	// 是否需要删除本层

		if deleteLevel{
			this.removeLevel(deleteNode, curLevel)
		}else{
			this.removeNode(deleteNode)
			curLevel++
		}

		deleteNode = nextDeleteNode
	}
	return originDeleteNode
}

// 移除最高层（仅当该层只有3个节点是才能移除本层），并移除deleteNode和上下节点的链接
func (this *SkipList) removeLevel(deleteNode *SkNode, curLevel int){
	head := deleteNode.left
	tail := deleteNode.right

	// 删除deleteNode的上下连接
	if deleteNode.up != nil{
		deleteNode.up.down = deleteNode.down
	}
	if deleteNode.down != nil{
		deleteNode.down.up = deleteNode.up
	}

	// 删除头尾节点的上下连接
	if this.maxLevel == curLevel{
		this.head = this.head.down
		this.tail = this.tail.down
		this.head.up = nil
		this.tail.up = nil
	}else{ // 删除的层不是最底层和最高层
		head.down.up = head.up
		head.up.down = head.down
		tail.down.up = tail.up
		tail.up.down = tail.down
	}
	this.maxLevel--
}

// 移除本层的某个节点
func (this *SkipList) removeNode(node *SkNode){
	// 删除左右链接
	node.left.right = node.right
	node.right.left = node.left

	// 删除上下连接
	if node.up != nil{
		node.up.down = node.down
	}
	if node.down != nil{
		node.down.up = node.up
	}
}

 

- 更新一个节点

func (this *SkipList) Update(oldData, newData int) *SkNode{
	this.Remove(oldData)
	return this.Insert(newData)
}

 

- 打印跳表

// 打印跳表
func (this *SkipList) Print(){
	curNode := this.head
	for curLevel:=this.maxLevel; curLevel>=1; curLevel--{
		head := curNode
		curNode = curNode.right
		for ; curNode.Value < math.MaxInt32; curNode = curNode.right{
			fmt.Printf("%d ", curNode.Value)
		}
		curNode = head.down
		fmt.Println()
	}
}

 

· 跳表复杂度

查询跳表节点的过程包括横向查找和纵向查找，因此首先要知道跳表的高度和每层的节点数。

已知跳表的每一层节点个数都是下一层的 1/2，而最底层节点数为n。

假设层数为 k（层数从上往下数，最顶层为第1层，且每层节点个数不算虚拟头结点和尾结点），则：

第k层节点数为n。 

第k-1层节点数为n/2。 

...

第1层节点数为 1。

所以 k ≈ log(n)。第 i 层节点数量为 2^(i-1)。

 

假设我要查找的节点刚好是最后一个节点，则在纵向上需要访问 k = log(n)个节点。

在横向上：

在第1层要访问1个节点，跨越了 1/2 * n 个节点，进入下一层。

在第2层要再访问1个节点，跨越了 1/4 * n 个节点，总共跨越了 3/4 * n个节点。

...

在第k层要再访问1个节点到达目标节点，跨越了 1个节点，总共跨越了 n 个节点。

因此 横向上跨越n个节点也需要遍历 k = log(n)个节点。

 

横向 + 纵向遍历的平均节点数 = log(n) + log(n) = 2log(n)

因此时间复杂度 为 O(log(n))。

 

同理，插入和删除的时间复杂度也是O(log(n))，用大T表示法插入和删除的复杂度也只比查询的复杂度多了一个T(log(n))，因为插入和删除是先进行查询再自底向上插入和删除层高次数的节点。

 

跳表的空间复杂度 = 第1层的节点数 + 第2层节点数 + ... + 第k-1层节点数 = 1 + 2 + ... + n/2 ≈ n。

因此 空间复杂度 为 O(n)。

 

综上，跳表的增删改查时间复杂度为 O(log(n))，空间复杂度为O(n)，而有序数组的查找复杂度为 O(log(n))，增删改时间复杂度为O(n)，不考虑数组扩展的情况下空间复杂度O(1)。

跳表属于典型的空间换时间。