图的遍历

图的遍历可以使用深度优先和广度优先遍历。

图的深度优先遍历做法和多叉树的深度优先遍历（前序遍历和后续遍历）一样，关键在于“回溯”，使用递归实现。

图的广度优先遍历做法和多叉树的层序遍历一样，关键在于“重放”（把遍历过的顶点按照之前的遍历顺序重新回顾（目的是记录它们并找到他们的相邻节点），就叫做重放），使用队列实现。

 

也就是说，图的深度优先遍历和广度优先遍历 和 树的深度、广度优先遍历的实现基本一致，唯一不同的是图的多个顶点可能成环，因此需要一个hashmap或者数组记录已经访问过的顶点，避免重复访问。

 

直接上代码，以遍历下面这个无向图为例

 

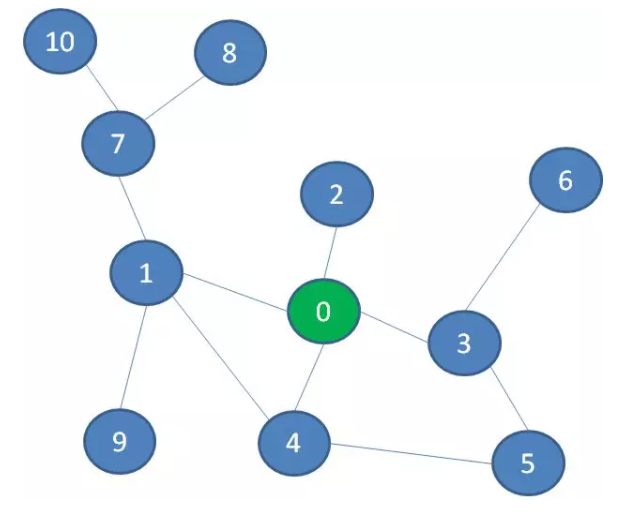
深度优先遍历

// 深度优先算法遍历有向图, 以二维数组形式表示邻接表
func DFSFromStart(arr [][]int, s int) []int{
	visited := make(map[int]struct{})
	res := make([]int, 0)

	var backtrack func (start int)
	backtrack = func(start int) {
		if len(arr[start]) == 0{    // 如果某个顶点没有它所指向的相邻节点则结束本分支的遍历，转而遍历图的其他分支
			return
		}

		if _, ok := visited[start]; ok{   // 如果start节点已经遍历过，则不再遍历start和start的相邻节点
			return
		}
		visited[start] = struct{}{}
		res = append(res, start)    // 将start顶点添加到结果列表中
		for _, neibor := range(arr[start]){  
			backtrack(neibor)   // 遍历 neibor 节点做在的分支
		}
	}
	backtrack(s)
	return res
}

 

广度优先算法

// 广度优先算法遍历有向图, 以二维数组形式表示邻接表，数组下标就是图节点，len(arr) = 10 表示有10个图节点
func BFSFromStart(arr [][]int, s int) []int{	// s表示出发节点，对于有向图而言，如果随便从某个节点出发，可能遍历不到整个图
	queue := list.New()		// 初始化一个队列
    visited := make(map[int]struct{})  // 放入到队列之前，标记该节点为已访问，或者说标记为已放入队列
	visited[s] = struct{}{}
	queue.PushBack(s)
	res := make([]int, 0)
	

	for queue.Len() > 0{
		first := queue.Front()
		queue.Remove(first)
		nodeVal := first.Value.(int)
		res = append(res,nodeVal)

		for _, neibor := range(arr[nodeVal]){
			if _, ok := visited[neibor]; ok{  // 标记为已放入队列的节点不再重复放入队列
				continue
			}
			visited[neibor] = struct{}{}
			queue.PushBack(neibor)
		}
	}
	return res
}

 

测试用例后面会汇总。

 

深度优先算法的应用：寻找两个顶点的所有路径

// 深度优先算法寻找两个节点的所有路径
func DFSFindAllPath(arr [][]int, s, e int) [][]int{
	allPath := make([][]int, 0)
	visited := make(map[int]struct{})	// 某条路径上已经遍历过的节点
	curPath := make([]int, 0)		// 当前遍历的某条路径

	var backtrack func (start int)
	backtrack = func(start int) {	// 从某个没有遍历过的节点start出发，计算到达e节点的路径的函数
		curPath = append(curPath, start)
		visited[start] = struct{}{}

		defer func(){
			// 回溯
			delete(visited, start)
			curPath = curPath[:len(curPath)-1]
		}()

		if start == e{	// 到达终点
			allPath = append(allPath, []int{})
			lastPathIdx := len(allPath)-1
			allPath[lastPathIdx] = append(allPath[lastPathIdx], curPath...)

			// 回溯
			//delete(visited, start)
			//curPath = curPath[:len(curPath)-1]
			return
		}

		for _, neibor := range(arr[start]){		// 寻找start的所有相邻节点到终点e的路径
			if _, ok := visited[neibor]; ok{
				continue
			}
			backtrack(neibor)
		}

		// 回溯
		//delete(visited, start)
		//curPath = curPath[:len(curPath)-1]
	}
	backtrack(s)
	return allPath
}

该算法复杂度为阶乘级别。当到达终点或者没有到达终点但是当前节点的所有节点都已经访问过则本层递归结束。

 

广度优先算法的应用：寻找两个顶点的最短路径

// 广度优先算法寻找两个节点的最短路径
func BFSFindMinPath(arr [][]int, s, e int) []int{
	queue := list.New()
	visited := make(map[int]int)	// value为key的上一层相邻节点，当找到目标e时，要通过visited找到从s到e的路径
	queue.PushBack(s)
	visited[s]= -1
	var curVext int	// 当前在遍历的顶点
	found := false	// 是否能找到目标节点e
	path := make([]int, 0)

	for queue.Len() > 0{
		found = false
		curLen := queue.Len()
		for i:=0; i<curLen; i++{	// 一次性将上一次的curVext的相邻顶点取出（可以看成是多叉树下 curVext的所有子节点）
			neiborNode := queue.Front()
			queue.Remove(neiborNode)
			curVext = neiborNode.Value.(int)
			if curVext == e{
				found = true
				break
			}

			// 将curVext的相邻节点（子节点）放入队列
			for _, neibor := range(arr[curVext]){
				if _, ok := visited[neibor]; ok{
					continue
				}
				visited[neibor] = curVext
				queue.PushBack(neibor)
			}
		}
		if found{
			break
		}
	}

	if !found{
		return path
	}

	// 后序遍历visited链表获取最短路径
	var iterMinPath func(start int)
	iterMinPath = func(start int){
		if start == -1{
			return
		}
		iterMinPath(visited[start])
		path = append(path, start)
	}
	iterMinPath(e)
	return path
}

该算法时间复杂度为 O(n)，空间复杂度为O(n)。

 

 

 测试用例

func TestGraph(t *testing.T) {
	graph := [][]int{
		{1, 2, 3, 4},
		{0, 4,7,9},
		{0},
		{0,5,6},
		{0, 1,5},
		{3, 4},
		{3},
		{1,8,10},
		{7},
		{1},
		{7},
	}

    fmt.Println(BFSFromStart(graph, 0))    //[0 1 2 3 4 7 9 5 6 8 10]
	fmt.Println(DFSFromStart(graph, 0))    //[0 1 4 5 3 6 7 8 10 9 2]
	fmt.Println(DFSFindAllPath(graph, 1, 2))	// [[1 0 2] [1 4 0 2] [1 4 5 3 0 2]]
	fmt.Println(BFSFindMinPath(graph, 6, 9))	// [6 3 0 1 9]
}