·排序

根据时间复杂度的不同，主流的排序算法可以分为时间复杂度为O(n*2)、O(nlogn)和线性复杂度3大类。

 

·冒泡排序法(O(n*2))

假如数组长度为n，冒泡排序需要交换n-1轮，每一轮的交换过程要借助一前一后两个指针p1,p2（实际上可以理解为是一个大小为1的滑动窗口），把相邻的这两个指针指向的元素两两比较，当arr[p1]>arr[p2]则交换两个元素的位置，当p[1]<=p[2]时则不交换位置，比较完之后p1,p2往后移动。这样我们可以始终保持p2位置的元素大于p1元素，当p2到达未交换区域的尾部，且本轮排序完成了最后一次p1和p2的交换后，p2就是未排序区中最大的元素，此时p2位置可归入已交换区域（已排序区域）的元素，把未交换区域-1，已交换区域+1。重复n-1轮之后，数组就变成了有序的。

 

详细过程如下

原数组：

 

一轮排序：

 

 

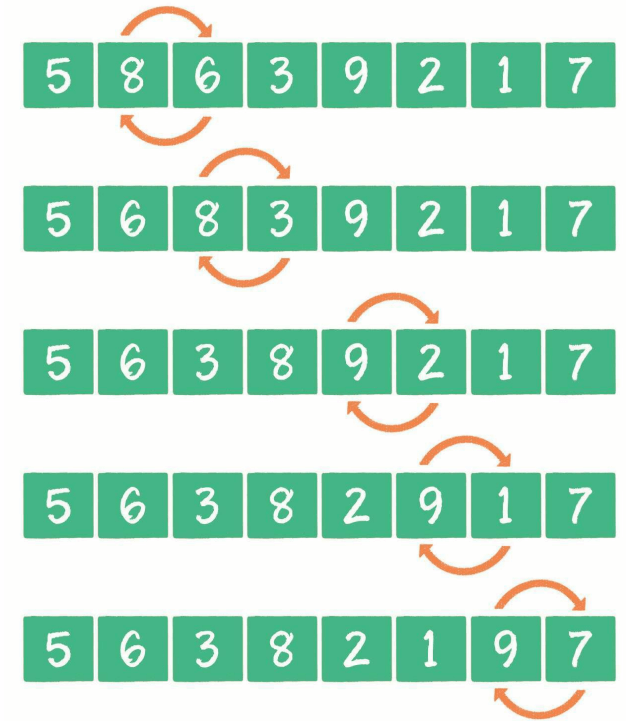
剩下的几轮排序：

 

我们可以将一个冒泡排序的序列分为已排序区（上图紫色区域）和未排序区（上图绿色区域）

 

下面是代码实现：

func BubbleSort(arr []int) []int{
	if len(arr) <= 1{
		return arr
	}

	end := len(arr) - 1			// end是未排序区的最后一个位置
	time, p1, p2 := end, 0, 1	// time是剩余要交换的轮数
	for time > 0 {
		time--
		for p2 <= end{
			if arr[p1] > arr[p2]{
				arr[p1], arr[p2] = arr[p2], arr[p1]
			}
			p1++
			p2++
		}
		p1 = 0
		p2 = 1
		end--
	}
	return arr
}

如何理解冒泡排序，其本质就是使用了前后双指针的技巧，这种写法是最容易理解的。

 

和上面思路相同的递归写法：

func BubbleSort3(arr []int){  // 该函数明确定义为：对完全未排序区域数组arr进行一轮排序
	if len(arr) <= 1{
		return
	}

	end := len(arr) - 1
	p1, p2 :=  0, 1

    // 开始本轮交换
	for p2 <= end{
		if arr[p1] > arr[p2]{
			arr[p1], arr[p2] = arr[p2], arr[p1]
		}
		p1++
		p2++
	}

	// 交换完一轮之后，通过递归交换下一轮，是一个前序遍历，但未排序区要缩小
	BubbleSort3(arr[:end])
}

 

下面是传统的写法：

func BubbleSort(sl []int) []int{
	for i:=1; i<=len(sl)-1; i++{	// 遍历n-1个节点(或者说要进行n-1轮排序)
		temp := 0
		for j:=0; j<len(sl) - i; j++{	// 每遍历一个节点要交换或比较n-i次, j是当前遍历到的节点下标
			if sl[j] > sl[j+1]{
				temp = sl[j+1]
				sl[j+1] = sl[j]
				sl[j] = temp
			}
		}
	}
	return sl
}

 

无论是哪种写法，都是外层循环控制交换的轮数，内层循环实施具体的交换操作。

 

 

下面是冒泡排序的几种优化：

优化1：

下面我们看看冒泡排序的优化，当完成了第6轮排序时，数组就已经排好了，但代码还是会去执行第7轮排序。

此时可以做个标记，如果某一轮排序中真正交换的次数为0则表示数组已经排好序，就无需完成剩下的几轮排序。

 

优化2：

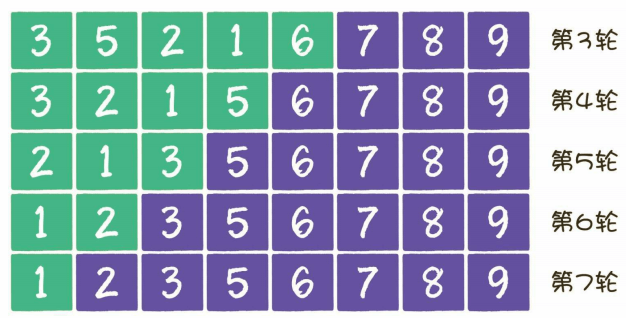
考虑下面这种情况

对于这样的一个数组而言，5678已经排好序，未排序的区域是前四个元素，按照冒泡排序算法，需要排序n-1=7轮。但实际如果只关注真正的未排序区，我们只用排序3轮。

此时我们需要找到这个有序区和无序区的边界并标记下来即可。

 

针对优化1和2的代码如下：

func BubbleSortImprove(arr []int) []int{
	if len(arr) <= 1{
		return arr
	}

	end := len(arr) - 1			// end是未排序区的最后一个位置
	p1, p2 := 0, 1	// time是剩余要交换的轮数
	for end > 0 {	// 当未排序区的分界下标end就是数组的第一个元素，即未排序区只有一个元素时，就可以停止下一轮交换
		fmt.Println(end)
		nextEnd := end - 1
		exchangeTime := 0	// 交换次数
		for p2 <= end{
			if arr[p1] > arr[p2]{
				arr[p1], arr[p2] = arr[p2], arr[p1]
				nextEnd = p1	// 只要交换了就说明分界要更新
				exchangeTime++
			}
			p1++
			p2++
		}
		if exchangeTime == 0{	// 如果某轮交换的交换次数为0，说明数组已经排好序
			return arr
		}
		p1 = 0
		p2 = 1
		end = nextEnd
	}
	return arr
}

增加了两个变量 nextEnd 和exchangeTime分别用来优化第二点和第一点。

 

优化3：

考虑一种情况，如果一个序列大部分元素已经排好序，按照传统的冒泡排序会执行很多无用的排序，如下所示

2~7其实已经排好了，但是冒泡排序依旧会执行7轮排序。但如果从右往左冒泡排序的话，排两轮就可以完成。为了优化这种情况，有人提出了鸡尾酒排序，其本质也是冒泡排序，按照第一轮从左到右排，第二轮从右到左排，像钟摆一样反复。

使用鸡尾酒排序，3轮冒泡就能排好。

func BubbleSortImprove2(sl []int) ([]int){
	temp := 0
	for i:=1; i<=len(sl)/2; i++{
		sorted := true
		for j:=i; j<len(sl)-i; j++{	// 从左到右排序
			if sl[j] > sl[j+1]{
				temp = sl[j+1]
				sl[j+1] = sl[j]
				sl[j] = temp
				sorted = false
			}
		}
		if sorted {
			break
		}
		sorted = true
		for j:=len(sl)-i; j>i; j--{  // 从右往左排序
			if sl[j] < sl[j-1]{
				temp = sl[j-1]
				sl[j-1] = sl[j]
				sl[j] = temp
				sorted = false
			}
		}
	}
	return sl
}

 

 

·选择排序法(O(n*2))

选择排序和冒泡排序的思路绝大部分一致，唯一不同点在于每轮比较如果arr[p1] > arr[p2]则不交换，每一轮排序中只需记录下该轮的未排序区的最大值下标A，将A与未排序区最后一个元素B交换，最后将元素B归入已排序区，即可进入下一轮排序。

 

对比选择排序和冒泡排序

相同点：

1、冒泡排序和选择排序的比较次数相同总共为 n*(n-1)/2次（都需要进行 n-1 轮比较，每轮进行平均 n / 2次比较），但是选择排序的交换次数小于冒泡排序。

最糟糕的情况下，冒泡排序的交换次数会和比较次数一样，达到 n*(n-1)/2，而选择排序的交换次数稳定为 n-1次。

因此，冒泡排序的比较次数和选择排序相同，但交换次数比选择排序多。

 

2、选择排序在数组包含多个相同值时，可能打乱相同值之间原有的顺序，而冒泡排序不会。下图为选择排序打乱相同值的一个例子（下图中是先将较小值放到前面，因此前面是已排序区，后面是未排序区）：

 

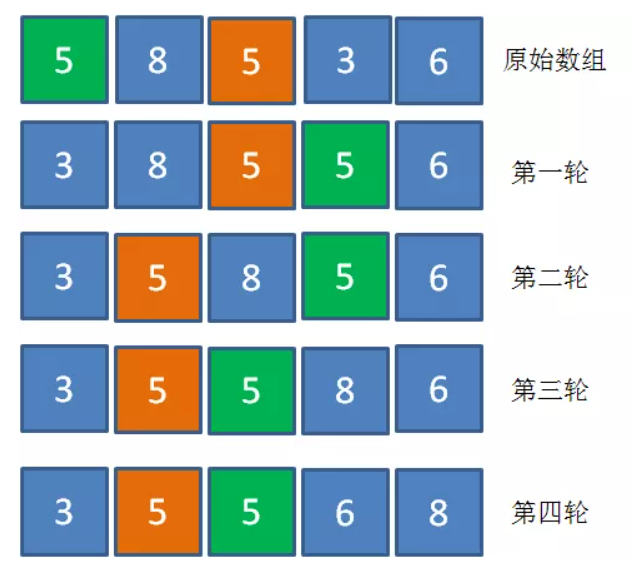
最终结论是：

通常情况下，选择排序由于交换次数少，性能略高于冒泡排序。但在要求保证相同值间原有顺序的特殊场景下必须使用冒泡排序。

此外，冒泡排序的交换次数在“数组中的大部分元素有序”时会变少很多，而选择排序的交换次数稳定为n-1，因此该情景下，冒泡排序的效率比选择排序高。

 

 

·插入排序

插入排序的思路是创建一个初始指向arr[0]的指针p，将数组arr分为：左边的已排序区（arr[:p]） 和 右边的未排序区（arr[p:]）。arr[p]是下一个要排好序的元素。

对arr进行n-1轮排序，每轮排序需要将arr[p]插入到排序区的合适位置（因此需要查找已排序区内arr[p]的合适位置，插入过程会导致已排序区内的部分元素整体后移）。

 

插入排序过程如下：

 

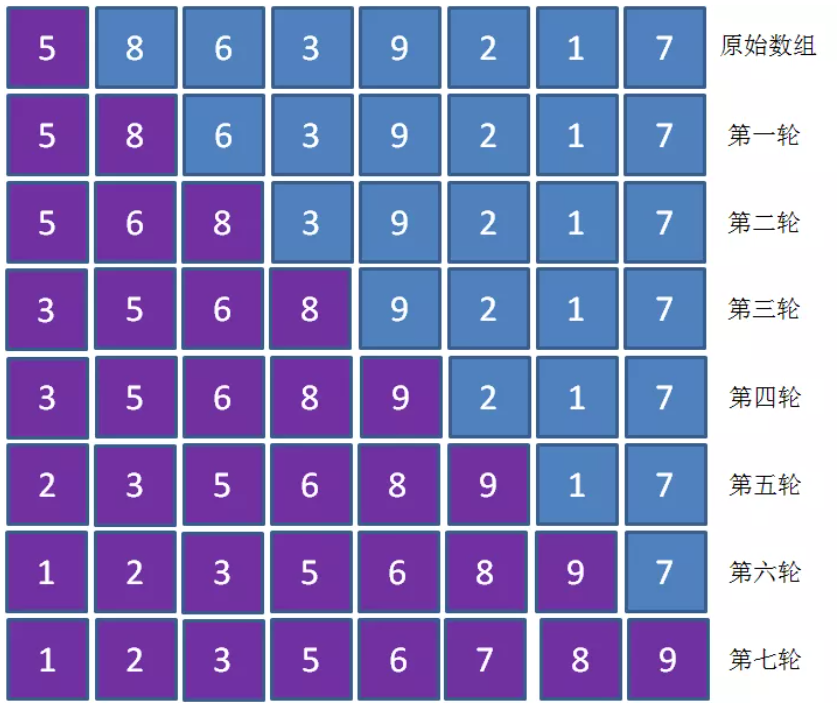
代码实现：

func InsertSort(arr []int) []int{
	p := 0
	for p < len(arr){
		target := arr[p]		// 要插入到已排序区的目标值
		i := p-1	// target要和[0, p-1]的数比较，从而找到要插入的位置，比较的同时要将arr[i]挪到arr[i+1]的位置
		for ; i >=0; i--{
			if target < arr[i]{
				arr[i+1] = arr[i]
			}else{		// 如果 arr[i] 比 arr[p]小或相等，则arr[p]插入到arr[i+1]的位置
				break
			}
		}
		arr[i+1] = target
		p++
	}
	return arr
}

 

在已排序区寻找arr[p]的合适插入位置是否可以使用二分查找降低复杂度？

肯定是不行的，因为将arr[p]插入到合适位置后，挪动已排序区内arr[p]后的元素也需要O(n)复杂度。

 

但相比于冒牌排序，插入排序不仅减少了很多次交换，也减少了很多次比较。

如果在数组大部分元素是有序的情况下，插入排序的比较次数和交换次数都可以大大减少（对一个完全排好序的数组进行插入排序其复杂度为O(n)），这是优于选择排序和冒泡排序的地方。