·二叉查找树（BST）

二叉查找树（又称二叉搜索树，二叉排序树）在二叉树的基础上增加了以下特点：

1、左子树所有节点小于根节点，右子树的所有节点大于根节点。

2、左右子树也都是二叉查找树

 

必须满足这两点的二叉树才是一个二叉搜索树。

 

·BST功能和使用场景

1、高效查找

对于一个节点分布相对平衡的二叉查找树，如果节点总数是n,那么查找节点的时间 复杂度就是O(logn)， 是树的深度。

 

2、维持节点有序性

由于左节点 < 根节点 < 右节点的特性，因此对BST中序遍历打印的值是升序的。因此二叉查找树又称为二叉排序树。

 

除了上面这些特性，还有一些比较细节的特性：对于一个树节点A，离A最近的比A小的节点是A的左子树的最右侧节点B，离A最近的比A大的节点是A的右子树的最左侧节点C：

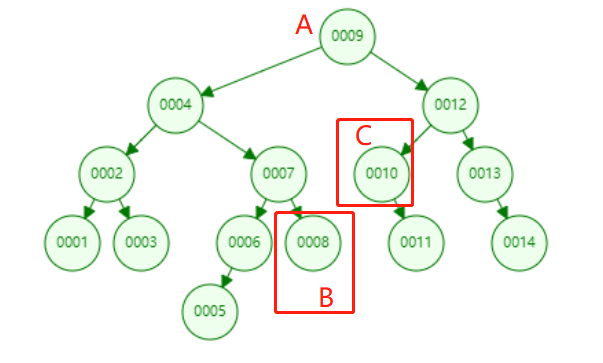
· BST的增刪查

// 二叉搜索树节点
type BST struct{
	Left *BST		// 左子树
	Right *BST		// 右子树
	Val int
}

func InitBST(val int) *BST{
	return &BST{Val:val}
}


// 二叉搜索树
type BstTree struct {
	root *BST
}



func InitBstTree() *BstTree{
	return &BstTree{}
}

这里没有直接使用BST节点表示一棵树（虽然树节点表示一棵树是可以的），而是使用BstTree表示一棵树，标明了树的根节点是root，这样做是因为如果直接用BST表示一棵树，删除的节点刚好是根节点时，需要将根节点 this 置为 nil，但这只是把方法内的指针置为nil，不会影响到方法外的树节点指针，结果就发现只剩下1个根节点时怎么删都删不掉。使用一个新的结构并标明root是根节点可以避免这种情况。

- 查找

从根节点开始查找，假设当前遍历到的节点值为val，查找目标值为target。判断target > val 则往val的右子树找，target < val 往val的左子树找，target == val 找到目标，如果到达叶子节点还未找到目标说明目标不存在。

该过程本质是在遍历一个单链表（树的任何一条路径其实就是一个链表）。

// 查找
func (this *BstTree) Find(target int) *BST{
	curNode := this.root		// 当前遍历指针
	for curNode != nil{
		if curNode.Val > target{
			curNode = curNode.Left
		}else if curNode.Val < target{
			curNode = curNode.Right
		}else{
			return curNode
		}
	}
	return nil
}

 

- 插入

插入操作其实本质上是先查找，找到节点要插入的正确位置后直接将父节点指针指向目标节点即可。需要注意的是插入的节点一定会被插入到叶子节点位置。

// 插入（非递归）
func (this *BstTree) Insert(target int){
	if this.root == nil{
		this.root = InitBST(target)
		return
	}
	pNode := this.root		// pNode是target节点的父节点
	for true{
		if pNode.Val > target{
			if pNode.Left == nil{
				pNode.Left = InitBST(target)
				break
			}
			pNode = pNode.Left
		}else if pNode.Val <= target{
			if pNode.Right == nil{
				pNode.Right = InitBST(target)
				break
			}
			pNode = pNode.Right
		}
	}
}

 

- 删除

分3种情况

1、待删除节点A是叶子节点直接删除即可；

2、待删除节点A只有一个子节点则用子节点取代被删除节点；

3、待删除节点A有两个子节点，此时需要用左子树或右子树中的一个子节点取代A，习惯上我们选择仅大于待删除节点的节点（也就是待删除节点的右子树的最左侧节点）来取代；

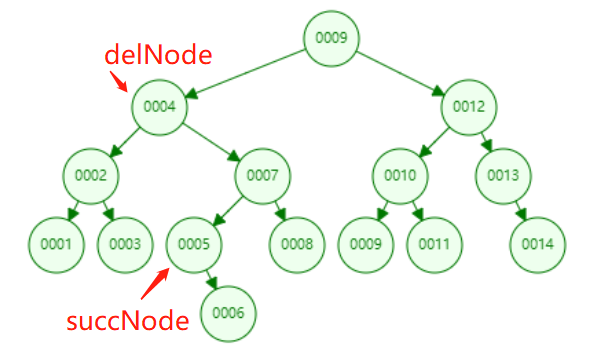
举个例子：图中要删除的节点是4，此时要用5作为替代节点（后继节点）

 

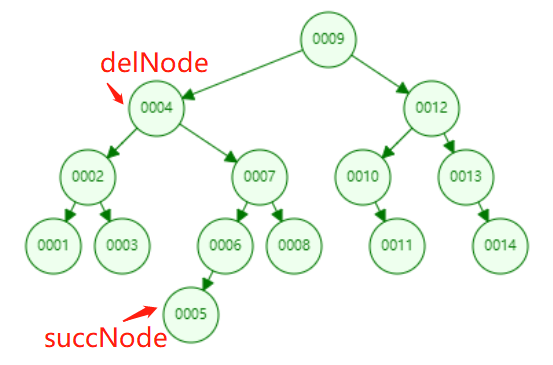
要删除的节点是4，替代节点为7

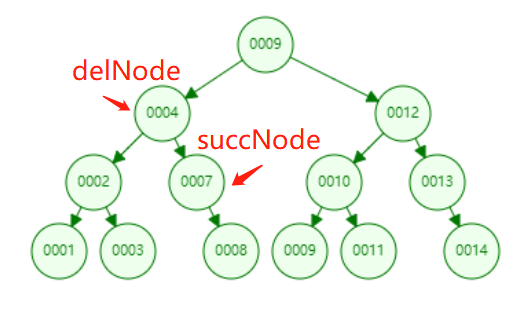
要删除的节点是4，替代节点为5

 

具体实现：

// 删除（非递归）
func (this *BstTree) Delete(target int) bool{
	if this.root == nil{
		return true
	}

	// 先查找要删除的节点及其父节点
	targetNode := this.root
	var pNode *BST
	isLeft := true

	for targetNode != nil{
		if targetNode.Val > target{
			pNode = targetNode
			targetNode = targetNode.Left
		}else if targetNode.Val < target{
			pNode = targetNode
			targetNode = targetNode.Right
		}else{
			// 找到节点，顺便判断是左节点还是右节点
			if pNode != nil && pNode.Left == targetNode{
				isLeft = true
			}else{
				isLeft = false
			}
			break
		}
	}

	if targetNode == nil{	// 说明这棵树不存在 target 这个值
		return false
	}

	// 删除target, 有3种情况：targetNode没有子节点，有一个子节点，有两个子节点，每种情况都要判断targetNode是根节点还是左节点还是右节点
	if targetNode.Left == nil && targetNode.Right == nil{	// targetNode是叶子节点
		if targetNode == this.root{
			this.root = nil
		}else if isLeft{
			pNode.Left = nil
		}else{
			pNode.Right = nil
		}
	}else if targetNode.Left == nil{	// targetNode只有右节点
		if targetNode == this.root{
			this.root = targetNode.Right
		}else if isLeft{
			pNode.Left = targetNode.Right
		}else{
			pNode.Right = targetNode.Right
		}
	}else if targetNode.Right == nil { // targetNode只有左节点
		if targetNode == this.root{
			this.root = targetNode.Left
		}else if isLeft{
			pNode.Left = targetNode.Left
		}else{
			pNode.Right = targetNode.Left
		}
	}else{	// targetNode有两个节点
		// 寻找后继节点（即取代待删除节点的节点）和后继节点的父节点
		succNode :=targetNode.Right
		var succPNode *BST
		for succNode.Left != nil{	// 寻找targetNode右子树的最左侧节点（当succNode没有左子节点时，他才是最左侧节点）
			succPNode = succNode
			succNode = succNode.Left
		}

		targetNode.Val = succNode.Val	// 把后继节点的val覆盖 到targetNode，但不移除targetNode，而是移除后继节点
		if succPNode == nil{	// succPNode == nil説明targetNode.Right没有左子节点，此时targetNode.Right就是后继节点
			targetNode.Right = succNode.Right
		}else{
			succPNode.Left = succNode.Right		// 移除后继节点
		}
	}
	return true
}

 

 

如果觉得Insert或者Delete内的逻辑比较复杂可以使用递归，它相比于迭代的新增和删除而言在思路上会更清晰和简单些：

// 插入（递归）
func (this *BstTree) Insert2(tree *BST, target int) *BST{	// 返回创建的新节点
	if this.root == nil{	// 当要往this.root插入节点，但this.root为nil时
		this.root = InitBST(target)
		return this.root
	}

	var newNode *BST
	if target < tree.Val{
		if tree.Left == nil{
			newNode = InitBST(target)
			tree.Left = newNode
		}else{
			newNode = this.Insert2(tree.Left, target)
		}
	}else if tree.Val <= target{
		if tree.Right == nil{
			newNode = InitBST(target)
			tree.Right = newNode
		}else{
			newNode = this.Insert2(tree.Right,target)
		}
	}
	return newNode
}


// 删除（递归）
func (this *BstTree) Delete2(target int) bool{
	// 寻找target
	if this.root == nil{
		return true
	}

	targetNode := this.root
	pNode := this.root
	found := false
	for targetNode != nil{
		if targetNode.Val == target{
			found = true
			break
		}
		pNode = targetNode
		if targetNode.Val > target{
			targetNode = targetNode.Left
		}else if targetNode.Val < target{
			targetNode = targetNode.Right
		}
	}

	if !found{		// 没找到要删除的节点
		return false
	}

	// 刪除节点
	this.deleteSon(pNode, targetNode)
	return true
}

// 删除pNode的子节点delNode
func (this *BstTree) deleteSon(pNode, delNode *BST){	// 返回删除节点后的子树
	if delNode.Left == nil && delNode.Right == nil{
		if delNode == this.root {	// 要删除的节点就是根节点
			this.root = nil
		}else if pNode.Left == delNode{		// 如果delNode是左节点
			pNode.Left = nil
		}else if pNode.Right == delNode{
			pNode.Right = nil
		}
		//return this
	}else if delNode.Left == nil{	// 被删除节点有右节点
		if delNode == this.root{
			this.root = delNode.Right
		}else if pNode.Left == delNode{
			pNode.Left = delNode.Right
		}else if pNode.Right == delNode{
			pNode.Right = delNode.Right
		}
		//return this
	}else if delNode.Right == nil{	// 被删除节点有左节点
		if delNode == this.root{
			this.root = delNode.Left
		}else if pNode.Left == delNode{
			pNode.Left = delNode.Left
		}else if pNode.Right == delNode{
			pNode.Right = delNode.Left
		}
		//return this
	}else{
		// 寻找deNode.Right中最小的节点作为取代节点（后继节点）
		succNode := delNode.Right
		succPNode := delNode			// 初始的后继节点的父节点是待删除节点
		for succNode.Left != nil{
			succPNode = succNode
			succNode = succNode.Left
		}

		delNode.Val = succNode.Val
		this.deleteSon(succPNode,succNode)
	}
}

 

 

·二叉搜索树的缺陷

在插入顺序是有序的情况下，二叉搜索树的左右子树会不平衡，严重的话会导致增删改查复杂度提升到O(n)。

 

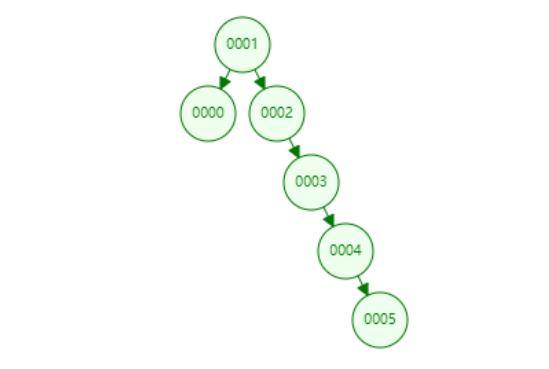
为了避免这种情况的发生，具有自动平衡功能的二叉平衡树和红黑树就出现了。