最短路径算法（Dijkstra 迪杰斯特拉算法 ）

对于一个加权无向图，如何求A到G的最短距离？

可以使用深度优先算法计算出所有从A到G的路径和最短距离，不过暴力解的时间复杂度为O(N!)

 

使用最短路径算法则可以在O(n^2)的时间复杂度算出图中任意两点的最短距离。

具体过程如下：

假设指定起点为A。

第1步，创建从A到图中其他顶点的距离表。表中的Key是顶点名称，Value是从起点A到对应顶点的已知最短距离。Value默认是无限大。

 

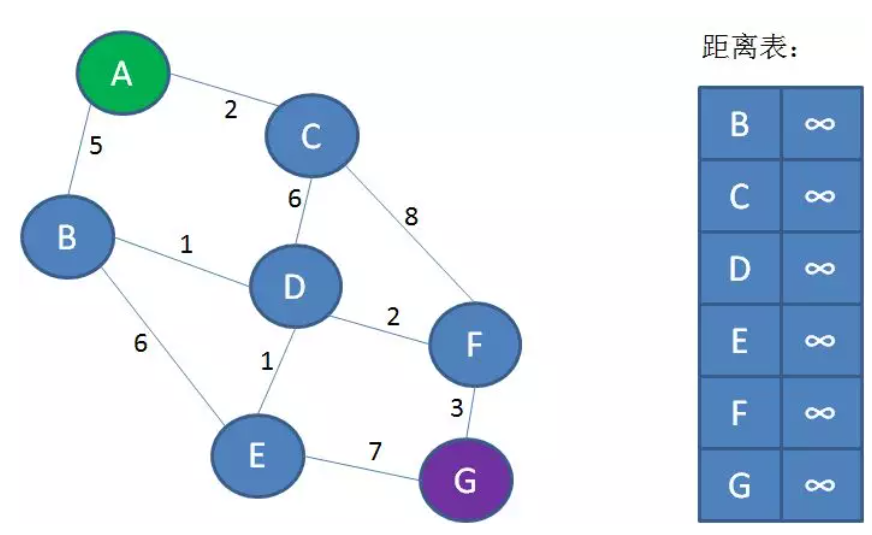
第2步，先计算起点A到A的所有相邻顶点 B和C的距离，更新到距离表中。

 

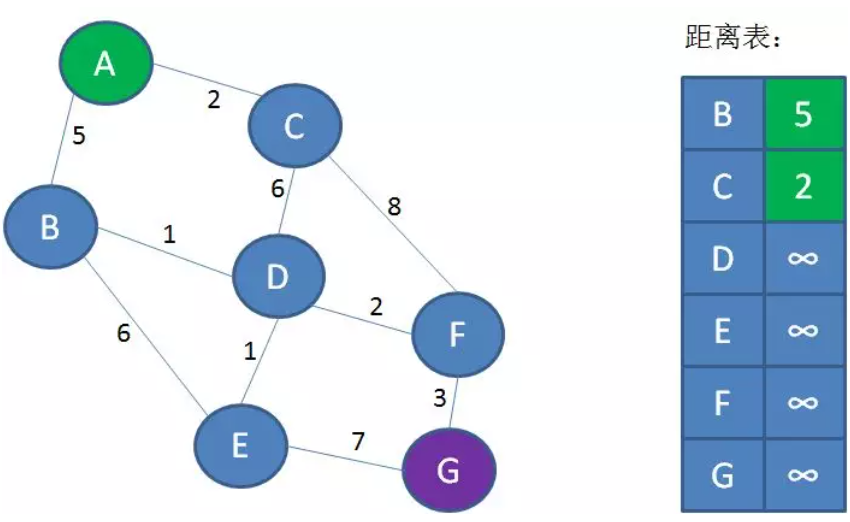
第3步，从距离表中找到离A最近的且没有访问过的节点，也就是C。将C标记为已访问。并且找到C相邻的所有节点（包括已访问过的和未访问过的） D 和 F，计算A到 D 和 F 的最短距离，如果这个距离比记录表中的A到D和F的距离更小，就将这个更小的距离更新到距离表中，否则不更新。

 

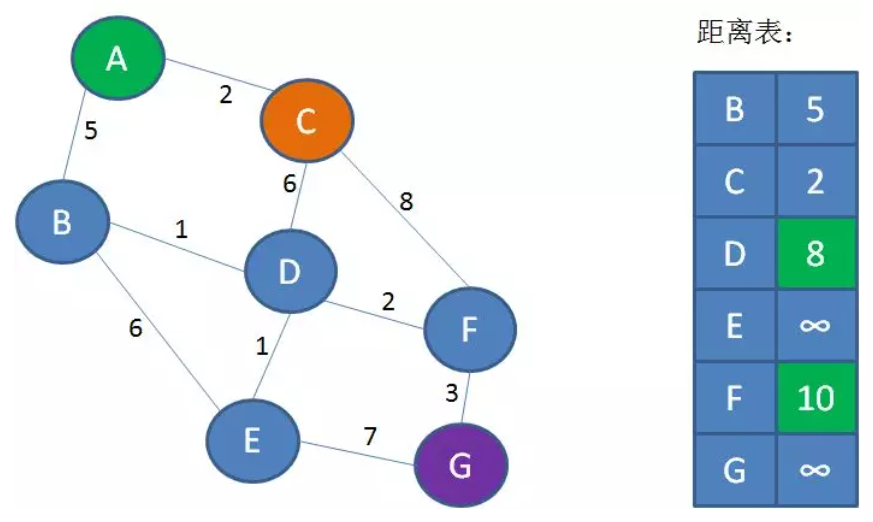
重复第3步的过程，直到所有节点都被遍历过，因此上述循环第3步的次数等于 n-1 次，即所有节点都被访问1次。

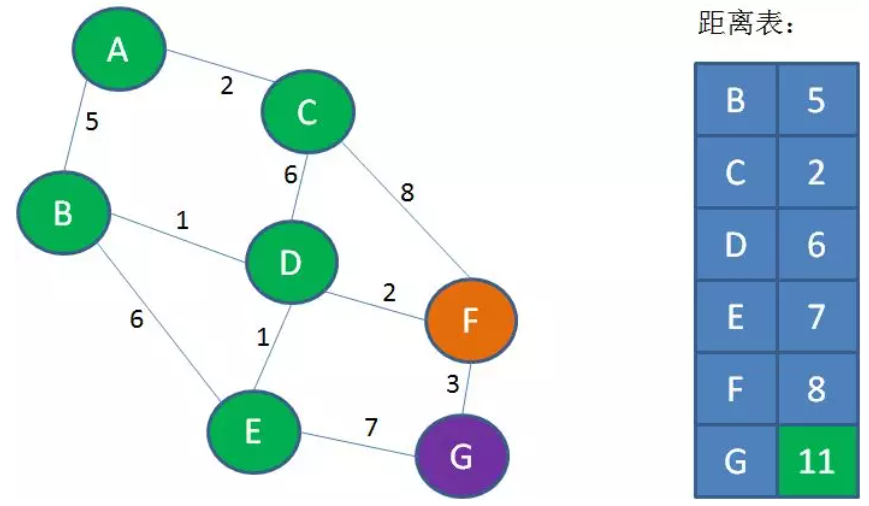
这么一来，不仅计算出了A到G的最短距离，还算出了A到所有节点的最短距离。

 

上面只得到了A到所有节点的最短距离，但是没有得到A到所有节点的路径，为此我们可以构建一个路径表（前置顶点表），路径表的key和距离表一样，只不过路径表的value表示从起点A到该节点的路径中，该节点的上一个节点。

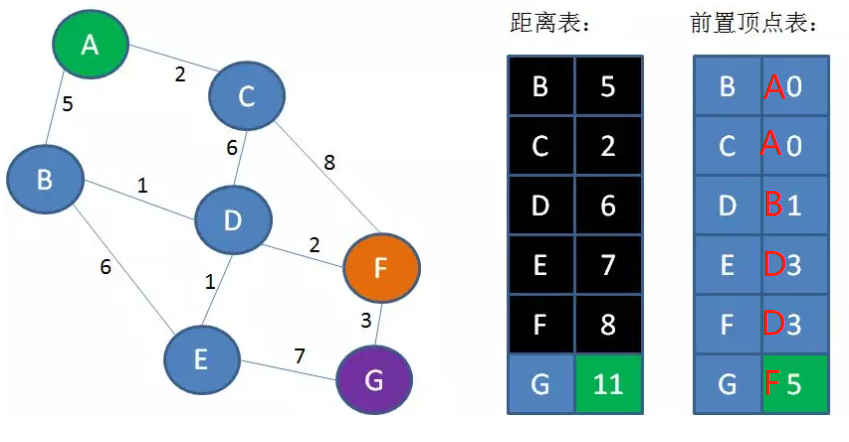
上图所示，A - G的路径为 ABDFG

假设路径表 path 是一个hashmap，如果想要求A - G 的最短路径详情，从path[G] 开始一直找到 A即可，这是一个对链表 G - F- D- B- A 进行后序遍历的过程。

 

代码实现

// 最短路径算法
func minPath(g map[*GNode][]int, s *GNode) (map[*GNode]int, map[*GNode]*GNode){
	num := len(g)		// 图中的总节点数
	visited := make(map[*GNode]struct{})
	res := make(map[*GNode]int)	// 距离表
	path := make(map[*GNode]*GNode)	// 路径表
	for k, _ := range(g){
		if k == s{
			continue
		}
		res[k] = math.MaxInt32
	}
	visited[s] = struct{}{}
	
	// 获取起点的所有相邻顶点，并更新他们的距离到 res 中
	for i, neibor := range(s.Neibors){
		res[neibor] = g[s][i]
		path[neibor] = s
	}

	// 遍历与 s 最近的未访问过的顶点N，生成s到N所有相邻顶点的最小距离
	for i:=1; i<num; i++{
		var vext *GNode		// 离s最近的顶点，也是本次循环要访问的顶点
		minDistance := math.MaxInt32	// s 和 vext的距离
		allVisited := true	// 距离表中所有的顶点都被访问过
		for node, distance := range(res){
			if _, ok := visited[node]; ok || distance == math.MaxInt32{	// 这两种顶点不访问：距离表中访问过的顶点 和 没有访问过但是距离s为无穷大的顶点（意味着s和该顶点不相通）
				continue
			}
			allVisited = false
			if minDistance > distance{
				minDistance = distance
				vext = node
			}
		}

		if allVisited{
			break
		}

		visited[vext] = struct{}{}
		for i, neibor := range(vext.Neibors){
			if neibor == s{
				continue
			}
			distance := minDistance + g[vext][i]	// s 离 neibor 的距离 = s 离 vext的距离 + vext 离 neibor 的距离
			if res[neibor] > distance{
				res[neibor] = distance
				path[neibor] = vext
			}
		}
	}
	return res, path
}

该算法用了嵌套循环，时间复杂度为O(n^2)。

 

下面是测试用例，用例按照上图中的图构建，0~6分别表示A~F。

func TestMinPath(t *testing.T) {
	graphVal := make([][][]int, 7)		// key 是 顶点的值， value是  顶点的相邻顶点以及它们对应的距离
	graphVal[0] = [][]int{{1, 5}, {2,2}}	// 0号节点和1号节点相邻，权重为5；0号节点和2号节点相邻，权重为2；
	graphVal[1] = [][]int{{0, 5}, {3,1}, {4,6}}
	graphVal[2] = [][]int{{0, 2}, {3,6}, {5,8}}
	graphVal[3] = [][]int{{1, 1}, {2,6}, {4,1}, {5,2}}
	graphVal[4] = [][]int{{1, 6}, {3,1}, {6,7}}
	graphVal[5] = [][]int{{2, 8}, {3,2}, {6,3}}
	graphVal[6] = [][]int{{4,7}, {5,3}}

	g := make(map[*GNode][]int)
	hmap := make(map[int]*GNode)
	for i, v := range(graphVal){
		var vext *GNode
		if _, ok := hmap[i]; ok{
			vext = hmap[i]
		}else{
			vext = initGNode(i)
			hmap[i] = vext
		}

		g[vext] = make([]int, 0)
		for _, neibor := range(v){
			var neiborNode  *GNode
			if _, ok := hmap[neibor[0]]; ok{
				neiborNode = hmap[neibor[0]]
			}else{
				neiborNode = initGNode(neibor[0])
				hmap[neibor[0]] = neiborNode
			}
			vext.Neibors = append(vext.Neibors, neiborNode)
			g[vext] = append(g[vext], neibor[1])
		}

	}

	res, path := minPath(g, hmap[0])
	for v, distance := range(res){
		fmt.Println(v, distance)
		fmt.Println(v, path[v])
	}

	fmt.Println()
	fmt.Println()
	fmt.Println()
	lastNode := hmap[6]		// 从起点到终点的路径中终点的上一个节点，初始lastNode默认是终点
	realPath := make([]*GNode, 0)
	for ;lastNode != hmap[0];lastNode = path[lastNode]{
		realPath =  append(realPath, lastNode)
	}
	realPath =  append(realPath, hmap[0])

	// 翻转 realPath
	for p1, p2 := 0, len(realPath) - 1; p1 < p2; p1, p2 = p1+1, p2-1{
		realPath[p1], realPath[p2] = realPath[p2], realPath[p1]
	}
	for _, v := range(realPath){
		fmt.Println(v.Val)
	}


	//&{6 [0xc0000045a0 0xc0000045e0]} 11
	//&{1 [0xc000004520 0xc000004580 0xc0000045a0]} 5
	//&{2 [0xc000004520 0xc000004580 0xc0000045e0]} 2
	//&{3 [0xc000004540 0xc000004560 0xc0000045a0 0xc0000045e0]} 6
	//&{4 [0xc000004540 0xc000004580 0xc000004640]} 7
	//&{5 [0xc000004560 0xc000004580 0xc000004640]} 8
}

 

如何进一步优化 最短路径算法？

在内层循环中，需要遍历路径表找到 与起点 s 最近的，且没有遍历过的顶点，这个过程是O(n)。其实可以多维护一个最小堆（初始最小堆为空），堆里面存放“没有遍历过的且s可到达的顶点（即距离表中value不为无穷大的顶点）”。如此一来整个程序的复杂度会降为 O(elogn)，e是边的条数。

 

如下图所示，B和C是外层循环已经遍历过的顶点，G是当前不可到达的顶点。

 

 

 

 

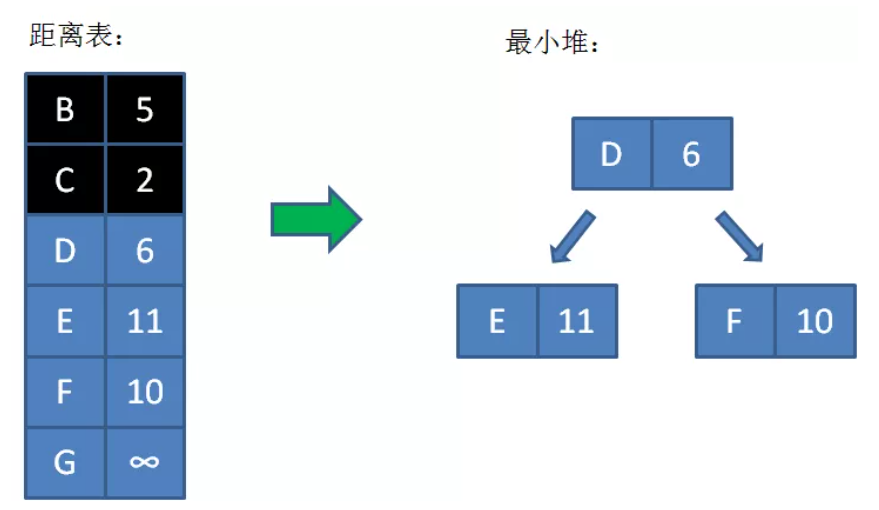
多源最短路径算法（弗洛伊德算法）

最短路径算法可以计算出有权无向图某顶点到其他任意顶点的最短距离。

如果题目要求 所有顶点两两之间的距离呢？

此时可以对每一个顶点使用最短路径算法，即可得到所有顶点两两之间的距离，然而还有一种实现起来更方便的方法，称为多源最短路径算法。

 

该算法的基本思路是

1. 先构建带权邻接矩阵，任意两个顶点 i 和 j 如果直接相连，那么他们之间的直连距离为 arr[i][j]；如果 两个顶点 不直接相连，即 i 需要经过一个或若干个中间顶点才能到达 j，那么他们之间的直连距离为 ∞。但即使 i 和 j是直接相连，i 和 j之间的直连距离不一定是他们的最短距离，有可能 i 经过其他中间节点到达 j 的距离更短。

 

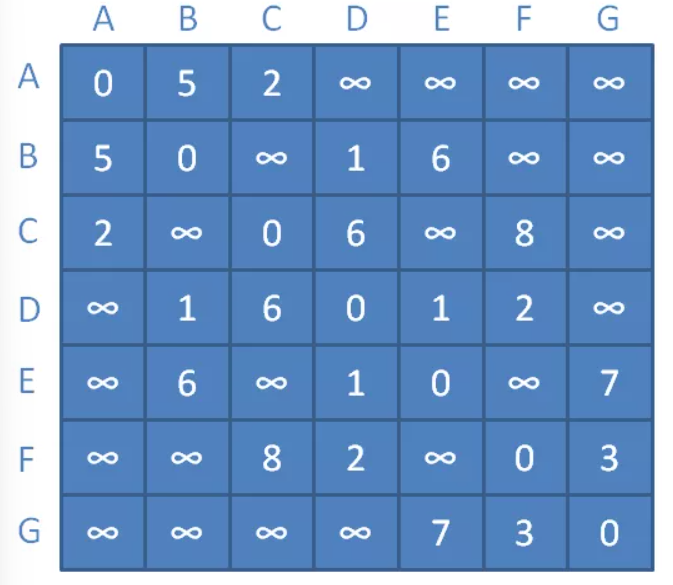
2. 所以，分别以 A~G 作为中间顶点（假设中间顶点为K∈[A, G]），那么顶点i 到 顶点j 的新距离 = Min（顶点i 到 顶点j 的旧距离，顶点i 到 顶点K 的距离+顶点K 到 顶点j 的距离）。

并将新距离更新到 arr[i][j] 和 arr[j][i]中。

对于任意的两个顶点 i，j，会发生 n 次更新过程。当所有顶点之间的距离都更新完毕，则邻接矩阵就变成了任意两个顶点的最短距离的二维数组。

 

可能大家一个疑问，如果i 和 j之间不只隔了一个节点，而是隔了多个节点，例如 A 和 B之间隔了 C 和 G两个节点（即 A - C - G - B），而且A 和 G不直接连通，C和B也不直接连通。那么初始状态下 以C作为中间节点无法计算出A和B的距离，因为 C-B之间的距离也是 无穷大。 同理以G作为中间节点也无法计算出A和B的距离，因为 A-G之间的距离也是 无穷大。

这么一来不就无法通过所谓的中间节点算出 A 和 B的过程了么？其实在程序运行的过程，会在某一轮循环计算出 A - C - G 的AG距离 或者 计算出 C - G - B的 CB距离。这么一来 AB的距离就能通过 C作为中间节点 或者 G作为中间节点算出。如果 A B 之间有n条路径，则用同一条路径上的任意一个中间节点算出的 AB距离都是相同的。

 

下面是代码实现：

// 多源最短路径算法
func multiMinPath(g [][]int) [][]int{	// g是邻接矩阵
	num := len(g)
	path := make([][]int, num)
	for i:=0; i<num; i++{		// 拷贝一份g到path
		p := make([]int, 0, num)
		p = append(p, g[i]...)
		path[i] = p
	}

	for k:=0; k<num; k++{	// 以 k 作为中间节点
		for i:=0; i<num; i++{
			for j:=0; j<num; j++{
				if path[i][k] == math.MaxInt32 || path[j][k] == math.MaxInt32{	// 如果 i 和 k 没有直接连通 或者 j 和 k没有直接连通
					continue
				}
				newDistance := path[i][k] + path[j][k]
				if path[i][j] > newDistance{
					path[i][j] = newDistance
				}
			}
		}
	}
	return path
}

 

测试用例

func TestMulMinPath(t *testing.T) {
	m := math.MaxInt32
	matrix := [][]int{
		{0,5,2,m,m,m,m},
		{5,0,m,1,6,m,m},
		{2,m,0,6,m,8,m},
		{m,1,6,0,1,2,m},
		{m,6,m,1,0,m,7},
		{m,m,8,2,m,0,3},
		{m,m,m,m,7,3,0},
	}
	fmt.Println(multiMinPath(matrix))  // 结果[[0 5 2 6 7 8 11] [5 0 7 1 2 3 6] [2 7 0 6 7 8 11] [6 1 6 0 1 2 5] [7 2 7 1 0 3 6] [8 3 8 2 3 0 3] [11 6 11 5 6 3 0]]
}