· BM算法

该算法的思路是：主串A和模式串B进行若干轮字符串比较，每轮从模式串B的尾部往前与A的子串进行比较，根据“坏字符”和“好后缀”规则一次性将B挪动多个位置从而减少比较的轮数。

RK算法是减小了每轮字符匹配的复杂度，BM算法则是直接减少了字符匹配的轮数。

 

BM算法定了两条规则：

坏字符规则 和 好后缀规则。

坏字符是指从后往前逐字符比较的过程中出现的第一个不相同的字符，坏字符是在A中的。

好后缀指A子串和B串本轮匹配成功的后缀串。

 

BM算法流程如下:

1、两个指针 i 和 j 分别指向 模式串B（长度n） 的尾部 和 主串A（长度m）的第n个位置。需要进行若干轮字符串匹配，每轮匹配是从后往前逐字符比较 B 和 与B等长的A子串。

 

2、每轮字符匹配过程如下：

a. 如果遇到 A[i] != B[j]，则 A[i] 就是主串A的坏字符，例如：

T是坏字符。此时需要找到 B中 j位置 开始往前的与坏字符相同的的第一个字符（从后往前顺序的第一个字符），并让这两个字符对齐，这样模式串 B 连续挪动了多位，节省了很多轮字符匹配：

 

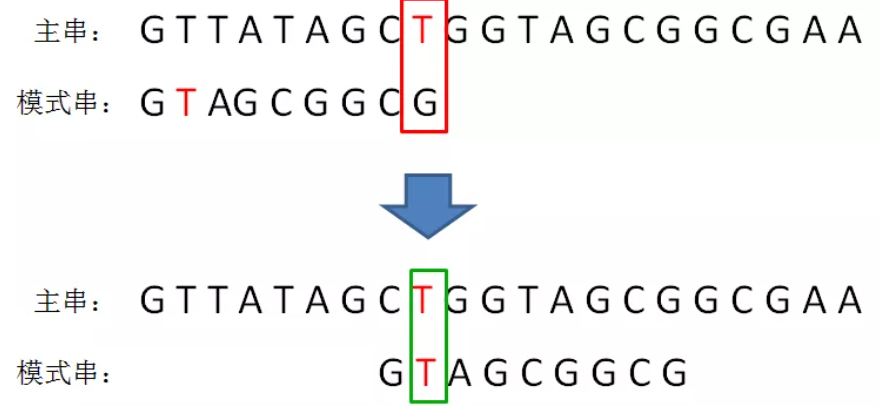
又例如

 

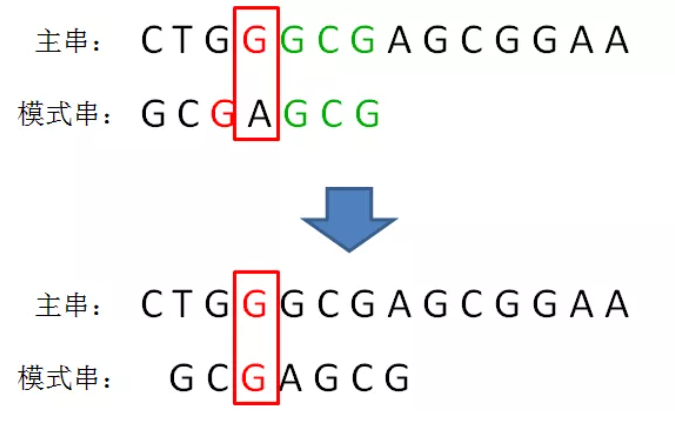
b. 如果 模式串B 在 j位置 之前的字符不存在坏字符，则直接把模式串挪到A的坏字符之后的第一个位置：

这样做是因为，B不存在坏字符，所以本轮A子串不可能存在某个后缀串是B的前缀串。

以上内容就是 坏字符规则。坏字符规则之所以要这样对齐是因为：A的某个子串如果和B串相同，则他们的相同字符肯定是对齐的。

 

c. 找到坏字符之后，查找 B 中 j位置往前是否存在和 好后缀 相同的串X，有则让 A中好后缀与B的串X对齐：

 

 

 

 

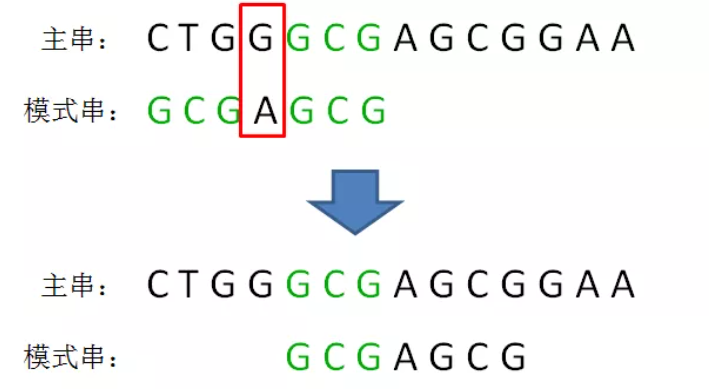
d. 如果 B 在j位置前的范围M内不存在与好后缀相同的子串，则判断范围M的前缀 是否是 好后缀的后缀，是则对齐：

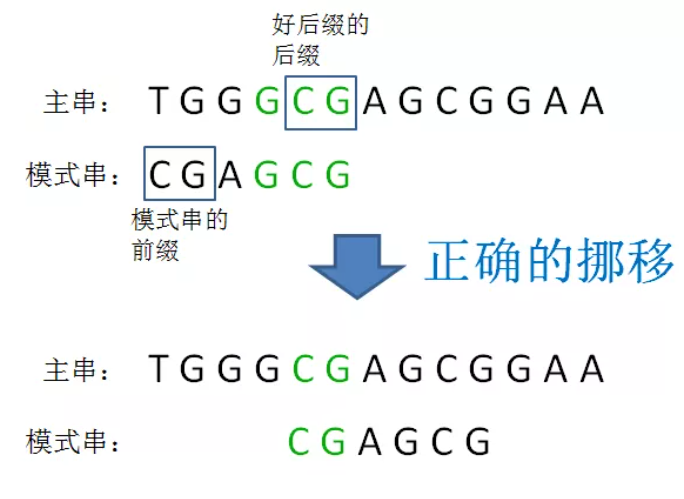
以上就是好后缀规则的内容。之后进入下一轮字符匹配。

 

什么情况下使用坏字符规则方法对齐，什么情况下使用好后缀规则方法对齐？

每轮字符匹配后，按照坏字符规则和好后缀规则分别计算需要挪动的距离，哪种距离更长，就把模式串挪动对应的长度。挪动的长度越多，节省的字符匹配轮数越多。

 

下面是只实现了坏字符规则的BM算法：

func BM(a, b string) int{	// 主串 a 和 模式串 b
	lenA := len(a)
	lenB := len(b)
	start := 0
	des := lenA - lenB		// 最大的start，start超过des则说明找不到目标子串，取闭区间

	for start <= des {		// start是A子串的开头位于A的哪个位置
		idx := lenB - 1		// 从b的末尾往前遍历
		for idx >=0 {
			if b[idx] != a[start + idx]{
				break
			}
			idx--
		}
		if idx < 0 {	// 本轮匹配所有字符都比较完毕
			return start
		}

		offset := _getBMOffset(b, a[start + idx], idx)		// start的偏移量
		if offset == -1{
			start++
		}else{
			start += offset
		}
	}
	return -1
}

func _getBMOffset(b string, targetByte byte, start int) int{	// 返回targetByte和start的距离
	if start == 0{
		return -1
	}
	offset := 1
	for i:=start-1; i>=0; i--{
		if b[i] == targetByte{
			return offset
		}
		offset++
	}
	return offset
}

 

BM算法是一个不稳定的字符串查找算法，在最坏情况下（主串A具有周期性而且A的子串与模式串B的多数字符相似的情况下）时间复杂度为O(mn)，最好情况下时间复杂度为O(n/m)，正常情况下时间复杂度为O(n+m)。