请关注公众号


二分查找是一种针对有序数组基于分治算法的的快速查找算法。
· 二分查找的基本思路
在一个有序数组中找到中间值mid,将该中间值mid和目标值target比对,如果target > mid,则在target以左的子序列递归查找;如果target < mid,则在target以右的子序列递归查找;如果target = mid则返回target所在的下标。
二分搜索的常用场景有三种:寻找一个数、寻找左侧边界、寻找右侧边界。
下面直接给出二分搜索框架
func BinarySearch(arr []int, target int) int{
left := 0
right := ... // 左右指针
for ...{
mid := left + (right - left) / 2;
if arr[mid] > target{
right = ...
}else if arr[mid] < target{
left = ...
}else{
...
}
}
return ...
}
计算 mid 时需要防止溢出,代码中left + (right - left) / 2就和(left + right) / 2的结果相同,但是有效防止了left和right太大直接相加导致溢出。
- 最基础版本
最基础版本的二分搜索:查找数组中的某个数。
// 二分搜索基础版
func BinarySearch(arr []int, target int) int{
if len(arr) == 0{
return -1
}
left := 0
right := len(arr) - 1 // 左右指针
for left <= right{
mid := left + (right - left)/2
if arr[mid] > target{
right = mid - 1
}else if arr[mid] < target{
left = mid + 1
}else{
return mid
}
}
return -1 // 没找到
}
- 寻找左侧边界的二分搜索
如果arr中可能存在多个相同的数([1,2,2,2,3]),而且题目要求找出最左侧2的下标怎么办。最简单的方法就是先用上面的基础版二分搜索找到中间的2,再用线性搜索的方式找到最左边或右边的2,但这么一来就难以保证二分查找对数级的复杂度了。
最佳做法是:
当 target > mid时,令left = mid+1;
当 target < mid时,令right = mid-1;
当 target == mid时,令right = mid;
当搜索空间[left, right]缩小到left和right到两个指针重合时,循环结束。
循环结束时有两种情况:
· 如果target在数组中,则left == right == mid,arr[left] == arr[right ] == arr[mid] == target;
· 如果target不在数组中,又分为种情况,以target为2为例:
· 如果上一轮[left, right] 对应的value为 [3, 4],则target在left以左,本轮的 left > right,right在left左边(而且right可能已经溢出数组范围到达-1),arr[left] != target,且arr[left]> target。
· 如果上一轮[left, right] 对应的value为 [0, 1],则target在right以右,本轮的[left, right]为[1, 1], left = right,arr[left]!= target,且arr[left]< target。
· 如果上一轮[left, right] 对应的value为 [0, 3],则target在left和right之间,本轮的[left, right]为[3, 3], left = right,arr[left]!= target,且arr[left]> target。
综上 只要 arr[left] != target,说明target不在数组中;arr[left] == target,说明target在数组中,且下标 left 就是target的最左侧下标。
如图所示:
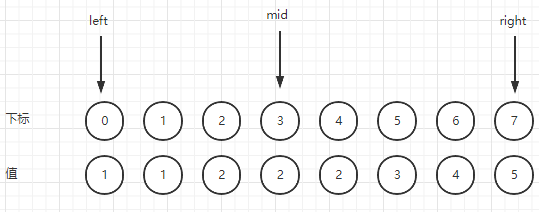
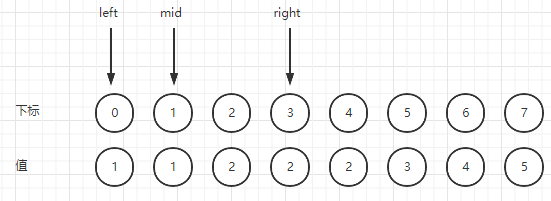
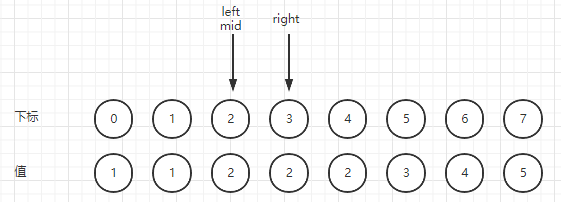
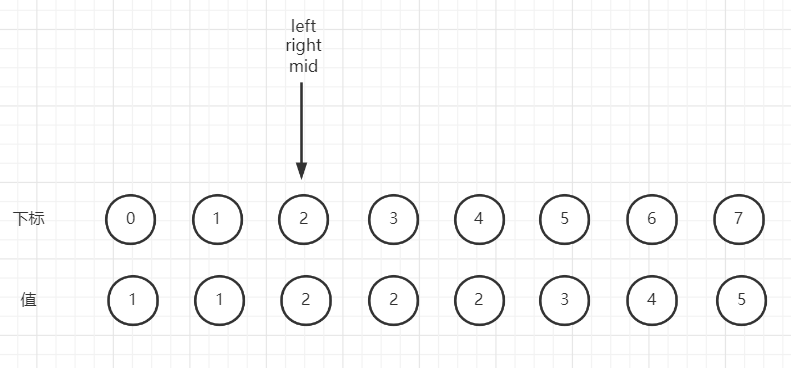
代码实现:
func BinarySearchLeft(arr []int, target int) int{
if len(arr) == 0{
return -1
}
left := 0
right := len(arr) - 1
for left < right{
mid := left + (right - left)/2
if target > arr[mid]{
left = mid + 1
}else if target < arr[mid]{
right = mid - 1
}else if target == arr[mid]{
right = mid
}
}
if arr[left] != target{ // 说明 arr 中不存在 target 值
return -1
}
return left
}
* 假设题目问的不是最左侧的target的位置,而是比target小的最近位置呢?*
只需找到最左侧的target的位置 p,p-1就是比target小的最近位置(如果 p-1<0,则说明不存在比target小的最近位置)。因此我们的实际目标还是为了找到最左侧target的位置p。
重点在于循环结束时的临界情况,此时有两种情况:
· 如果target在数组中,则left == right == mid,arr[left] == arr[right ] == arr[mid] == target,该情况下,解为 left - 1;
· 如果target不在数组中,又分为种情况,以target为2为例:
· 如果上一轮[left, right] 对应的value为 [3, 4],则本轮的 left > right,right在left左边(而且right可能已经溢出数组范围到达-1),arr[left] != target,且arr[left]> target,该情况下,解为 left - 1。
· 如果上一轮[left, right] 对应的value为 [0, 1],则本轮的[left, right]为[1, 1], left = right,arr[left]!= target,且arr[left]< target,该情况下,解为 left。
· 如果上一轮[left, right] 对应的value为 [0, 3],则本轮的[left, right]为[3, 3], left = right,arr[left]!= target,且arr[left]> target,该情况下,解为 left - 1。
综上 只要 arr[left] >= target,解为 left - 1(如果left==0,则left-1=-1,说明不存在这样的解);只要arr[left] < target,解为 left 。
代码实现如下:
func BinarySearchLess(arr []int, target int) int{
// ... 前面的代码省略,和上面的代码一样
if arr[left] >= target{
return left-1
}
return left
}
* 假设题目问是比target小或者和target相等的最近位置呢?*
此时如果 arr 存在target则优先选target的位置,不存在target则选比target小的位置。
func BinarySearchLessOrEqual(arr []int, target int) int{
// ... 前面的代码省略,和上面的代码一样
if arr[left] > target{
return left-1
}
return left
}
- 寻找右侧边界的二分搜索
和寻找左侧边界的二分搜索同理,唯一不同的地方在于,之前取mid都是 (left + right) /2 向下取整,这次变成向上取整,取到的mid离right比离left近。直接上代码
func BinarySearchRight(arr []int, target int) int{
if len(arr) == 0{
return -1
}
left := 0
right := len(arr) - 1
for left < right {
mid := left + (right - left + 1)/2 // 或者这里写成 left + (right - left)/2, 下面target == arr[mid]时写成 left = mid + 1也可
if target > arr[mid]{
left = mid + 1
}else if target < arr[mid]{
right = mid - 1
}else if target == arr[mid]{
left = mid
}
}
if arr[right] != target{ // 说明 arr 中不存在 target 值
return -1
}
return right
}
· 使用二分查找解题
什么问题可以运用二分搜索算法技巧?
首先,你要从题目中抽象出一个自变量x,一个关于x的函数f(x),以及一个目标值target。
同时,x, f(x), target还要满足以下条件:
1、f(x)必须是在x上的单调函数(单调增单调减都可以)。
2、题目是让你计算满足约束条件f(x) == target时的x的最值。
上文的【搜索左侧边界】就是符合这些条件的题目,它要求找到数组中等于target的最小下标,即求 f(x) = target时的最小x。
应对这种题目我们可以将代码框架写出,只要有题目符合上述条件就可以套用这个框架:
// 函数 f 是关于自变量 x 的单调函数
int f(x int) {
// ...
}
// 主函数,在 f(x) == target 的约束下求 x 的最值
func solution(nums []int, target int) int{
if (len(nums) == 0) return -1
left := 0;
right := len(nums) - 1
for left < right {
mid := left + (right - left) / 2; // 或者 mid := left + (right - left + 1) / 2
if (f(mid) == target) {
// left = mid 或者 right = mid
} else if (f(mid) < target) {
// left = mid + 1 或者 right = mid - 1
} else if (f(mid) > target) {
// right = mid - 1 或者 left = mid + 1
}
}
// ... 最终判断条件
}
套用框架前必须注意4点:
1、动笔前明确题目需求
具体用区间法来表示,假设题目给出临界值为t,题目的需求可以是求 target ∈ [t, t] 下的下标(寻找某一个数),也可以是求 target ∈ [t, +∞) 的下标(寻找最左侧目标)。一般离不开以下几种(以升序而言):
A.target ∈ [t, t] (寻找某一个数t)
B.target ∈ [t, +∞) (寻找最左侧的t,如果t不在数组中则取比t大的离t最近的目标的下标,即转为了情况C)
C.target ∈ (t, +∞) (寻找比t大的离 t 最近的目标) 等价于 target ∈ [t+1, +∞)
D.target ∈ (-∞, t] (寻找最右侧的t,如果t不在数组中则取比t小的离t最近的目标的下标,即转为了情况E)
E.target ∈ (-∞, t) (寻找比t小的离 t 最近的目标) 等价于 target ∈ (-∞, t-1]
在开始写代码前,我会必须要求自己写出这样的一个区间式子来表达题目的需求。
2、for表达式一定要写成 left < right,因为这样可以在left和right重合时停止循环,避免了left溢出(left = len(arr))或者right溢出(right = -1),也节省了for循环之后判断溢出这个步骤。
3、for结束后,arr[left]分为3种情况:
arr[left] < target
arr[left] == target
arr[left] > target
需要结合“题目的需求”判断每种情况(必须3种情况都判断)该取的真正下标(真正下标可能是 left / left+1 / left-1 中的一种或两种)。
4、当arr长度为偶数时,mid的取值需要斟酌取中间偏左的下标还是中间偏右的下标,这是为了避免当搜索范围[left, right]只剩2个元素时,触发 f(mid) == target 运行left = mid 或者 right = mid之后,left/right的位置不变,导致死循环。
二分查找的相关题目可以参考:力扣:二分搜索练习题
力扣875. 爱吃香蕉的珂珂
珂珂喜欢吃香蕉。这里有 N 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 H 小时后回来。
珂珂可以决定她吃香蕉的速度 K (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 K 根。如果这堆香蕉少于 K 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 H 小时内吃掉所有香蕉的最小速度 K(K 为整数)。

分析:本题的自变量x是 K,target为H,求 f(K) = H时的最小K。速度K增大,H就会越小,因此 H是K的递减函数。
二分查找的题目第一步先找出自变量的范围,本题中K的最小值是 piles 的最小值,K的最大值是piles的最大值,因此K的范围是 [1, max(piles)],令f(K) = H 的最小K就在 [1, max(piles)] 这个范围之内。
我们可以 将范围内的自变量一个个带入到 K 变量中进行验算,从而找到最小K,如此一来验算的次数为n次。更好的方法就是使用二分查找,将 范围中的mid值带入到K变量验算,这样验算的次数减少为logn。
由于时间H是速度K的减函数,因此while循环内的 if res > h/ res < h/ res== h 这3中情况下要做的事情(如 left = mid+1、right=mid-1等)比较难判断,此时可以画一个坐标图来判断:
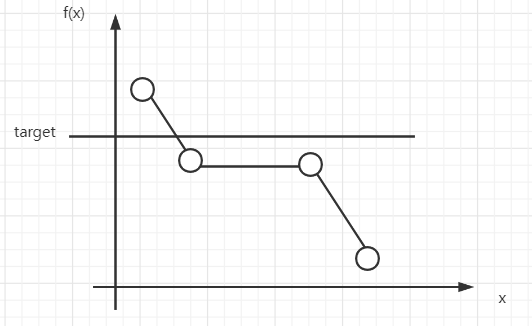
代码实现:
# coding=utf-8
from math import ceil
class Solution:
def minEatingSpeed(self, piles, h):
self.piles = piles
left = piles[0]
right = piles[-1]
while left < right:
mid = left + (right - left) / 2 # mid是速度speed
res = self.calculate(mid)
if res > h:
left = mid + 1
elif res < h:
right = mid - 1
else:
right = mid
res = self.calculate(left)
if res <= h :
return left
return left - 1
def calculate(self, speed):
hours = 0
for pile in range(self.piles):
hours += ceil(pile / speed)
return hours
力扣1011. 在 D 天内送达包裹的能力
传送带上的包裹必须在 D 天内从一个港口运送到另一个港口。
传送带上的第 i 个包裹的重量为 weights[i]。每一天,我们都会按给出重量的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。
返回能在 D 天内将传送带上的所有包裹送达的船的最低运载能力。

分析:
这也是一道速度和时间的题目,速度就是载重能力。题目求最小载重能力,因此载重能力(速度)就是自变量x,target是天数,因此天数(时间)就是因变量f(x)。题目要求 f(x) = target 下最小的x,和上一题基本一样。
运载能力x的最小值是 max(weights),最大值是 sum(weights)。
代码实现:
from math import floor
class Solution:
def shipWithinDays(self, weights, days):
left = 0 # left是自变量(运载速度)的最小值,即max(weights)
right = 0 # right是自变量(运载速度)的最大值,即sum(weights)
for weight in weights:
if left < weight:
left = weight
right += weight
while left < right:
midSpeed = left + floor((right - left) / 2)
curRes = self.calculate(weights, midSpeed)
if curRes > days:
left = midSpeed + 1
elif curRes < days:
right = midSpeed - 1
else:
right = midSpeed
curRes = self.calculate(weights, left)
if curRes <= days:
return left
return left+1
def calculate(self, weights, speed):
days = 0
curWeight = 0 # 当前负载
for weight in weights:
if curWeight + weight <= speed:
curWeight += weight
else:
curWeight = weight
days += 1
days += 1
return days
